题目内容
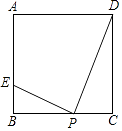
【题目】(11分)已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
(1)如图1,当△ABC是等边三角形时,请你写出满足图中条件,四个成立的结论;
(2)如图2,当△ABC中只有∠ACB=60°时,请你证明S△ABC与S△ABD的和等于S△BCE与S△ACF的和.


【答案】(1)答案不唯一,如:DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点;(2)见解析
【解析】试题分析:(1)由等边三角形的性质可写出结论.
(2)要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
试题解析:(1)DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点;
(2)过A作AM∥FC交BC于M,连接DM、EM,
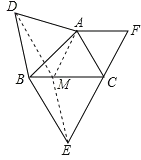
∵∠ACB=60°,∠CAF=60°,
∴∠ACB=∠CAF,
∴AF∥MC,
∴四边形AMCF是平行四边形,
又∵FA=FC,
∴四边形AMCF是菱形,
∴AC=CM=AM,且∠MAC=60,
∵在△BAC与△EMC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△BAC≌△EMC,
∵∠DAM=∠DAB+∠BAM=60°+∠BAM,
∠BAC=∠MAC+∠BAM=60°+∠BAM,
∴∠BAC=∠DAM
在△ABC和△ADM中
AB=AD,∠BAC=∠DAM,AC=AM,
∴△ABC≌△ADM(SAS)
故△ABC≌△MEC≌△ADM,
在CB上截取CM,使CM=CA,
再连接AM、DM、EM
易证△AMC为等边三角形,
在△ABC与△MEC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△ABC≌△MEC(SAS),
∴AB=ME,∠ABC=∠MEC,
又∵DB=AB,
∴DB=ME,
∵∠DBC=∠DBA+∠ABC=60°+∠ABC,
∠BME=∠BCE+∠MEC=60°+∠MEC,
∴∠DBC=∠BME,
∴DB∥ME,
即DB与ME平行且相等,故四边形DBEM是平行四边形,
∴四边形DBEM是平行四边形,
∴S△BDM+S△DAM+S△MAC=S△BEM+S△EMC+S△ACF,
即S△ABC+S△ABD=S△BCE+S△ACF.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案