Question

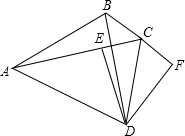如图△ABC中，AB的垂直平分线与∠ACB的外角平分线交于点D，DE⊥AC于E，DF⊥BC于E则下列结论：①△ADE≌△BDF：②AE=CE+CB；③∠ADB=∠ACB；④∠DCF+∠ABD=90°，其中一定成立的是

1. A.
   ①②③
2. B.
   ①②④
3. C.
   ②③④
4. D.
   ①②③④

Answer 1

A
分析：①根据角平分线的性质与线段垂直平分线的性质，可得DE=DF，∠F=∠AED=90°，AD=BD，然后利用HL，即可判定①正确；
②首先在EA上截取EM=EC，然后利用AAS即可判定△AMD≌△ACD，根据全等三角形的对应边相等，即可判定AE=CE+CB；
③利用全等三角形的对应角相等与等腰三角形的性质，即可求得∠ADB=∠ACB；
④利用三角形的外角的性质与全等三角形的对应角相等的知识，可证得∠DCF=∠ABD，但不能证得∠DCF+∠ABD=90°．
解答：①∵DC是∠ACB的外角平分线，DE⊥AC，DF⊥BC，
∴DE=DF，∠F=∠AED=90°，
∵D在AB的垂直平分线上，
∴AD=BD，
∴Rt△ADE≌Rt△BDF（HL），
故①正确；
②在EA上截取EM=EC，
∵DE⊥AC，∠MDE=∠CDE，
∴DM=DC，
∵∠CDE=∠CDF，
∴∠CDF=∠EDM，
∵Rt△ADE≌Rt△BDF，
∴∠DAM=∠DBC，∠ADE=∠BDF，
∴∠ADM=∠CDB，
∴△AMD≌△ACD（AAS），
∴AM=BC，
∴AE=AM+ME=BC+EC；
故②正确；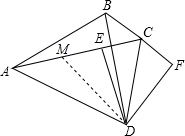
③∵DM=DC，
∴∠DMC=∠DCM=∠DCF，
∵∠ACB+∠ECD+∠DCF=180°，∠DMC+∠DCM+∠MDC=180°，
∴∠MDC=∠ACB，
∵∠ADM=∠BDC，
∴∠ADB=∠ADM+∠MDB=∠MDB+∠CDB=∠MDC，
∴∠ADB=∠ACB；
故③正确；
④∵∠EMD=∠MAD+∠MDA，
∵∠BAC=∠MDA，
∴∠EMD=∠MAD+∠BAC=∠DAB，
∵AD=BD，DM=CD，
∴∠ABD=∠DAB，∠CMD=∠MCD，
∴∠MCD=∠ABD，
∵∠DCF=∠MCD，
∴∠FCD=∠ABD，
∴∠ECF+∠FCD=∠ABD+∠FCD≠90°，
故④错误．
故正确的有：①②③．
故选A．
点评：此题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质以及线段垂直平分线的性质等知识．此题综合性较强，难度较大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．