题目内容
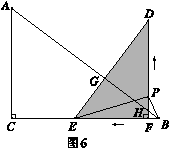
如图1,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm.在Rt△DEF中,∠DFE=90°,EF=6cm,
DF=8cm.E,F两点在BC边上,DE,DF两边分别与AB边交于G,H两点.现固定△ABC不动,△DEF从点F
与点B重合的位置出发,沿BC以1cm/s的速度向点C运动,点P从点F出发,在折线FD—DE上以2cm/s的速
度向点E运动.△DEF与点P同时出发,当点E到达点C时,△DEF和点P同时停止运动.设运动的时间是
t(单位:s),t>0.
(1)当t=2时,PH= cm ,DG = cm;
(2)t为多少秒时△PDE为等腰三角形?请说明理由;
(3)t为多少秒时点P与点G重合?写出计算过程;
(4)求tan∠PBF的值(可用含t的代数式表示).
DF=8cm.E,F两点在BC边上,DE,DF两边分别与AB边交于G,H两点.现固定△ABC不动,△DEF从点F
与点B重合的位置出发,沿BC以1cm/s的速度向点C运动,点P从点F出发,在折线FD—DE上以2cm/s的速
度向点E运动.△DEF与点P同时出发,当点E到达点C时,△DEF和点P同时停止运动.设运动的时间是
t(单位:s),t>0.
(1)当t=2时,PH= cm ,DG = cm;
(2)t为多少秒时△PDE为等腰三角形?请说明理由;
(3)t为多少秒时点P与点G重合?写出计算过程;
(4)求tan∠PBF的值(可用含t的代数式表示).

(1)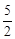 ,
,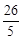
(2)只有点P在DF边上运动时,△PDE才能成为等腰三角形,且PD=PE.(如图6)
∵ BF=t,PF=2t,DF=8,
∴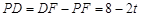 .
.
在Rt△PEF中,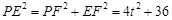 =
=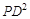 .
.
即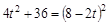 .
.
解得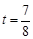 .
.
∴ t为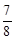 时△PDE为等腰三角形.
时△PDE为等腰三角形.
(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP= DG.
由已知可得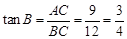 ,
,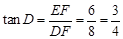 .
.
∴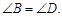
∴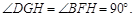
∴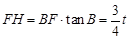 ,
,
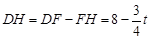 ,
,
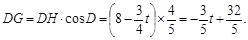
∵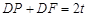 ,
,
∴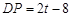 .
.
由DP=DG得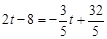 .
.
解得 .
.
检验: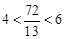 ,此时点P在DE边上.
,此时点P在DE边上.
∴ t的值为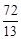 时,点P与点G重合.
时,点P与点G重合.
(4)当0<t≤4时,点P在DF边上运动(如图6),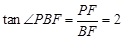 .
.
当4< t≤6时,点P在DE边上运动(如图7),作PS⊥BC于S,则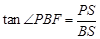 .
.
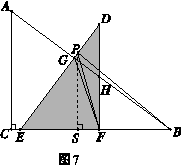
可得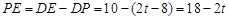 .
.
此时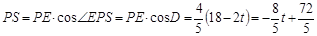 ,
,
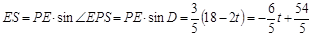 .
.
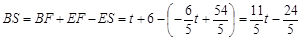 .
.
∴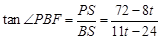
综上所述,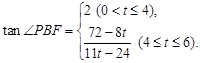
(以上时间单位均为s,线段长度单位均为cm)
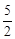 ,
,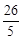
(2)只有点P在DF边上运动时,△PDE才能成为等腰三角形,且PD=PE.(如图6)

∵ BF=t,PF=2t,DF=8,
∴
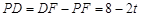 .
.在Rt△PEF中,
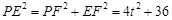 =
=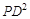 .
.即
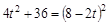 .
.解得
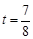 .
.∴ t为
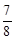 时△PDE为等腰三角形.
时△PDE为等腰三角形. (3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP= DG.
由已知可得
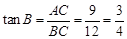 ,
,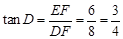 .
.∴
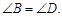
∴
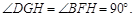
∴
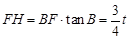 ,
,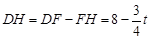 ,
,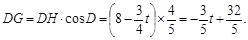
∵
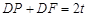 ,
,∴
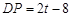 .
.由DP=DG得
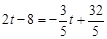 .
. 解得
 .
. 检验:
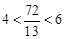 ,此时点P在DE边上.
,此时点P在DE边上.∴ t的值为
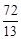 时,点P与点G重合.
时,点P与点G重合.(4)当0<t≤4时,点P在DF边上运动(如图6),
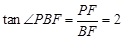 .
.当4< t≤6时,点P在DE边上运动(如图7),作PS⊥BC于S,则
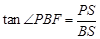 .
.
可得
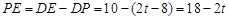 .
.此时
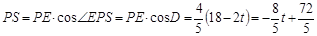 ,
,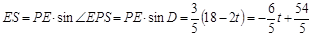 .
.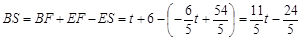 .
.∴
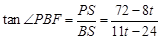
综上所述,
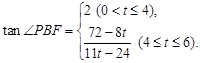
(以上时间单位均为s,线段长度单位均为cm)
(1)当t=2,得到BF=2,PF=4,根据BF:BC=HF:AC,即可求出HF,从而得到PH;BE=8,利用Rt△BEG∽Rt△BAC,可求出EG,得到DG;
(2)根据题意得到PD=PE,则BF=t,PF=2t,DF=8,得到PD=DF-PF=8-2t.在Rt△PEF中,利用勾股定理得到4t2+36=(8-2t)2,解得t=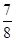 .
.
(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=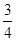 ,则FH=
,则FH=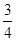 t,DH=8-
t,DH=8-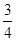 t,得到DG=-
t,得到DG=-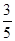 t+
t+ ,而DP+DF=2t,于是有2t-8=-
,而DP+DF=2t,于是有2t-8=-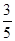 t+
t+ ,即可解得t的值;
,即可解得t的值;
(4)分类讨论:当0<t≤4时,点P在DF边上运动,tan∠PBF=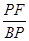 =2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF=
=2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF=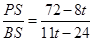 .
.
(2)根据题意得到PD=PE,则BF=t,PF=2t,DF=8,得到PD=DF-PF=8-2t.在Rt△PEF中,利用勾股定理得到4t2+36=(8-2t)2,解得t=
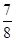 .
.(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=
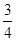 ,则FH=
,则FH=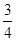 t,DH=8-
t,DH=8-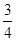 t,得到DG=-
t,得到DG=-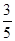 t+
t+ ,而DP+DF=2t,于是有2t-8=-
,而DP+DF=2t,于是有2t-8=-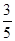 t+
t+ ,即可解得t的值;
,即可解得t的值;(4)分类讨论:当0<t≤4时,点P在DF边上运动,tan∠PBF=
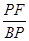 =2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF=
=2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF=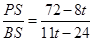 .
.
练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
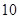 米的C处,用测角仪测得旗杆顶部A的仰角为
米的C处,用测角仪测得旗杆顶部A的仰角为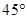 .已知测角仪器的高CD=
.已知测角仪器的高CD=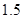 米,则旗杆AB的高是___________米.
米,则旗杆AB的高是___________米.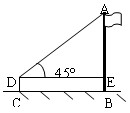
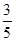
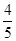
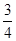
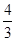
 如图那样折叠,使点
如图那样折叠,使点 与点
与点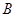 重合,折痕为
重合,折痕为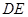 ,则
,则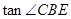 的值是___。
的值是___。
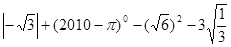 .
.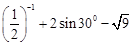 .
.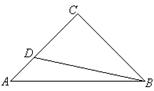
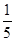 ,则sin∠CBD值为
,则sin∠CBD值为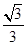 B.
B.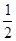
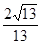 D.
D.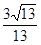
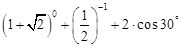
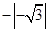
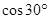 = .
= .