题目内容
如图,在平面直角坐标xOy中,一次函数 的图象与反比例函数
的图象与反比例函数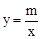 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,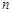 ).线段OA=5,E为x轴上一点,且sin∠AOE=
).线段OA=5,E为x轴上一点,且sin∠AOE= .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
 的图象与反比例函数
的图象与反比例函数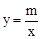 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,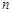 ).线段OA=5,E为x轴上一点,且sin∠AOE=
).线段OA=5,E为x轴上一点,且sin∠AOE= .
.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
(1)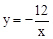 ,
,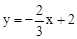 (2)6
(2)6
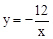 ,
,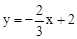 (2)6
(2)6解:(1)过点A作AD⊥x轴于D点,如图, 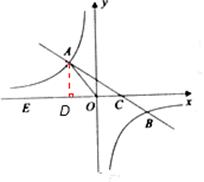
∵sin∠AOE= ,OA=5,∴sin∠AOE=
,OA=5,∴sin∠AOE=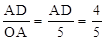 。
。
∴AD=4,∴DO=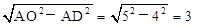 。
。
而点A在第二象限,∴点A的坐标为(-3,4)。
将A(-3,4)代入 ,得m=-12,
,得m=-12,
∴所求的反比例函数的解析式为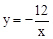 。
。
将B(6,n)代入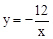 ,得n =-2。
,得n =-2。
将A(-3,4)和B(6,-2)分别代入 ,得
,得
 ,解得
,解得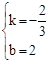 。
。
∴所求的一次函数的解析式为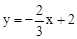 。
。
(2)在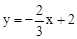 中,令y=0,即
中,令y=0,即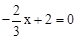 ,解得x=3。
,解得x=3。
∴C点坐标为(0,3),即OC=3,
∴ 。
。
(1)过点A作AD⊥x轴于D点,由sin∠AOE= ,OA=5,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-3,4),把A(-3,4)代入
,OA=5,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-3,4),把A(-3,4)代入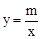 ,即可确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入
,即可确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入 ,即可确定一次函数函数的解析式。
,即可确定一次函数函数的解析式。
(2)先令y=0,求出C点坐标,得到OC的长,然后根据三角形的面积公式计算△AOC的面积即可。

∵sin∠AOE=
 ,OA=5,∴sin∠AOE=
,OA=5,∴sin∠AOE=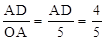 。
。∴AD=4,∴DO=
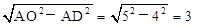 。
。而点A在第二象限,∴点A的坐标为(-3,4)。
将A(-3,4)代入
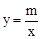 ,得m=-12,
,得m=-12,∴所求的反比例函数的解析式为
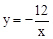 。
。将B(6,n)代入
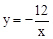 ,得n =-2。
,得n =-2。将A(-3,4)和B(6,-2)分别代入
 ,得
,得 ,解得
,解得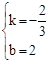 。
。∴所求的一次函数的解析式为
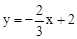 。
。(2)在
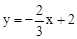 中,令y=0,即
中,令y=0,即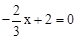 ,解得x=3。
,解得x=3。∴C点坐标为(0,3),即OC=3,
∴
 。
。(1)过点A作AD⊥x轴于D点,由sin∠AOE=
 ,OA=5,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-3,4),把A(-3,4)代入
,OA=5,根据正弦的定义可求出AD,再根据勾股定理得到DO,即得到A点坐标(-3,4),把A(-3,4)代入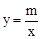 ,即可确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入
,即可确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入 ,即可确定一次函数函数的解析式。
,即可确定一次函数函数的解析式。(2)先令y=0,求出C点坐标,得到OC的长,然后根据三角形的面积公式计算△AOC的面积即可。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 的图像经过点(3,-4),则这个函数的解析式为 .
的图像经过点(3,-4),则这个函数的解析式为 .
 (
( ,
, )的图象经过点
)的图象经过点 (1,2),
(1,2), (
( ,
, )(
)( ),过点B作
),过点B作 轴的垂线,垂足为C.
轴的垂线,垂足为C.
 时,求点B的坐标;
时,求点B的坐标; 随的增大而减小的是( )
随的增大而减小的是( )

 (
( )
) (
( )
)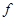 (度)是车速
(度)是车速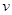 (km/h)的反比例函数,求
(km/h)的反比例函数,求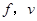 之间的关系式,计算当车速为100km/h时视野的度数.
之间的关系式,计算当车速为100km/h时视野的度数. ,下列说法不正确的是( )
,下列说法不正确的是( ) 时,
时, 随
随 的增大而增大
的增大而增大 时,
时, 、
、 、
、 的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( )
的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( ) 