题目内容
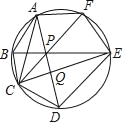
【题目】如图,圆内接六边形ABCDEF中AB=CD=EF,且三条对角线AD、BE、CF交于点P,CE与AD交于点Q,已知AC=26,CE=39,那么CQQE=_____.
【答案】324
【解析】
利用相似三角形的性质证明![]() =
=![]() =
=![]() =
=![]() =
=![]() ,设CQ=4k,QE=9k,构建方程求出k即可解决问题;
,设CQ=4k,QE=9k,构建方程求出k即可解决问题;
解:连AE,
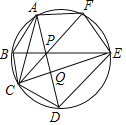
∵AB=CD=EF,
∴弧AB=弧CD=弧EF,
∴∠AEB=∠CED,
∴∠PED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC,
又∵∠PDE=∠ACE,
∴△PDE∽△ACE,
∴![]() =
=![]() ,
,
∵弧CD=弧EF,
∴DE∥CF,
∴![]() =
=![]() ,∠CPD=∠PDE,
,∠CPD=∠PDE,
∵∠PED对BD弧,∠ADC对AC弧,
而DC弧=AB弧,
∴∠PED=∠ADC,
∴△PDC∽△DEP,
∴![]() =
=![]() ,即PC=
,即PC=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
由(1)的结论 ![]() =
=![]() 得,
得,![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
设CQ=4k,EQ=9k,
则有13k=39,
∴k=3,
∴CQ=12,EQ=27,
∴CQQE=324,
故答案为324.

练习册系列答案
相关题目
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?