题目内容
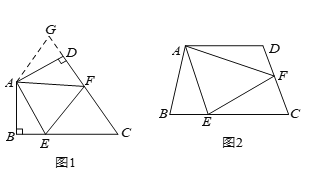
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向
向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向
向![]() 点运动.
点运动.

(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
【答案】(1)全等,理由见解析;(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为
的运动速度为![]() 时,能够使
时,能够使![]() 与
与![]() 全等
全等
【解析】
(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等,则可知PB=3tcm,PC=83tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
(1)经过1秒后,![]() ,
,![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中,
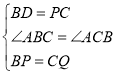 ,
,
![]() .
.
(2)设点![]() 的运动速度为
的运动速度为![]() ,经过
,经过![]() 与
与![]() 全等;则可知
全等;则可知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
根据全等三角形的判定定理![]() 可知,有两种情况:①当
可知,有两种情况:①当![]() ,
,![]() 时,②当
时,②当![]() ,
,![]() 时,两三角形全等;
时,两三角形全等;
①当![]() 且
且![]() 时,
时,![]() 且
且![]() ,解得
,解得![]() ,
,![]() ,
,![]() 舍去此情况;
舍去此情况;
②![]() ,
,![]() 时,
时,![]() 且
且![]() ,解得:
,解得:![]() ;
;
故若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为
的运动速度为![]() 时,能够使
时,能够使![]() 与
与![]() 全等.
全等.

练习册系列答案
相关题目
【题目】小明利用所学函数知识,对函数![]() 进行了如下研究.列表如下:
进行了如下研究.列表如下:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |

(1)自变量x的取值范围是________;
(2)表格中:m=_______;n=________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______________.
的图象交点的坐标为_______________.