题目内容
【题目】如图,AD是△ABC的角平分线,点F、E分别在边AC、AB上,连接DE、DF,且∠AFD+∠B=180°.
(1)求证:BD=FD;
(2)当AF+FD=AE时,求证:∠AFD=2∠AED.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)过点D作DM⊥AB于M,DN⊥AC于N,由角平分线的性质得DM=DN,角角边证明△DMB≌△DNF,由全等三角形的性质求得BD=FD;
(2)在AB上截取AG=AF,连接DG.由边角边证△ADF≌△ADG,根据全等三角形的性质得FD=GD,∠AFD=∠AGD,因AF+FD=AE,AE=AG+GE得FD=GD=GE,由等腰三角形等边对等角和三角形的外角定理得∠AGD=2∠GED,等量代换得∠AFD=2∠AED.
证明:(1)过点D作DM⊥AB于M,DN⊥AC于N,
如图1所示:
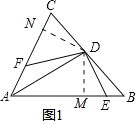
∵DM⊥AB,DN⊥AC,
∴∠DMB=∠DNF=90°,
又∵AD平分∠BAC,
∴DM=DN,
又∵∠AFD+∠B=180°,
∠AFD+∠DFN=180°,
∴∠B=∠DFN,
在△DMB和△DNF中,
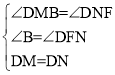
∴△DMB≌△DNF(AAS)
∴BD=FD;
(2)在AB上截取AG=AF,连接DG.
如图2所示,
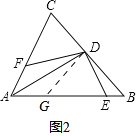
∵AD平分∠BAC,
∴∠DAF=∠DAG,
在△ADF和△ADG中.
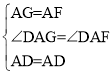 ,
,
∴△ADF≌△ADG(SAS).
∴∠AFD=∠AGD,FD=GD
又∵AF+FD=AE,
∴AG+GD=AE,
又∵AE=AG+GE,
∴FD=GD=GE,
∴∠GDE=∠GED,
又∵∠AGD=∠GED+∠GDE=2∠GED,
∴∠AFD=2∠AED.

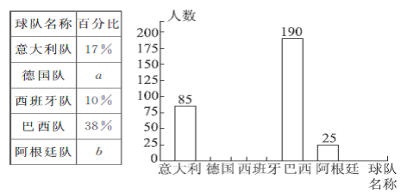
【题目】青少年“心理健康”问题已经引起了社会的关注,某中学对全校850名学生进行了一次“心理健康”知识测试,并从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本,列出下面的频数分布表(单位:分)
成绩 | 50.5≤x<60.5 | 60.5≤x<70.5 | 70.5≤x<80.5 | 80.5≤x<90.5 | 90.5≤x<100.5 |
频数 | 2 | 8 | 10 | 16 | 14 |
(1)组距是 ,组数是 .
(2)成绩在60.5≤x<80.5范围的频数是 .
(3)画出频数分布直方图.
(4)若成绩在80分以上(不含80分)为优秀,试估计该校成绩优秀的有多少人?