题目内容
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).
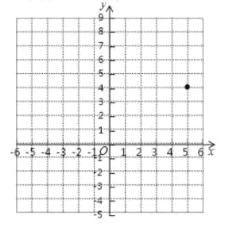
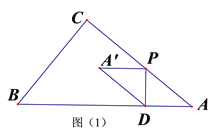
(1)画出△ABC,并求△ABC的面积.
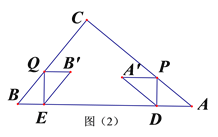
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
【答案】(1)见解析;(2)见解析,A′(﹣1,8),B′(2,1);(3)﹣9,1.
【解析】
(1)根据各点在坐标系中的位置描出各点,并顺次连接即可,面积利用矩形面积减去三角形面积求解;
(2)根据图形平移的性质画出平移后的△A′B′C′,并写出点A′,B′的坐标即可;
(3)根据点平移的性质即可得出m、n的值.
解:
(1)如图,△ABC即为所求
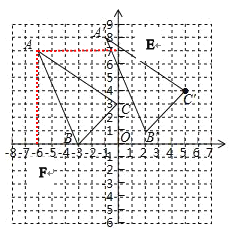 ;
;
作辅助线,过AF⊥x轴,垂足是F, AE⊥y轴,垂足是E.
△ABC的面积=S矩形AFOE-S△AFE- S△BCO- S△AEC
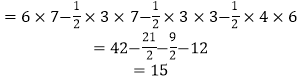
即面积是15.
(2)C(0,3)经过平移后的对应点为C′(5,4),则C点即为,向上平移1个单位,向右平移5个单位,相应的A,B,也一样平移即可得到:如图,△A′B′C′即为所求,A′(﹣1,8),B′(2,1);
(3)∵P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),
∴n=﹣3+4=1,m+6=﹣3,
∴n=1,m=﹣9.
故答案为:﹣9,1.

【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?