题目内容
【题目】如图,在平面直角坐标系中,已知正方形ABCD,点A(2,0),B(0,4),那么点C的坐标是___.

【答案】(﹣4,2).
【解析】
如图,作CE⊥y轴于点E,根据已知条件得到OA=2,OB=4,根据四边形ABCD是正方形,得到∠ABC=90°,BC=BA,根据余角的性质得到∠CBE=∠BAO,根据全等三角形的性质得到BE=OA=2,CE=OB=4,求得OE=OB﹣BE=4﹣2=2,于是得到结论.
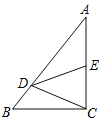
如图,作CE⊥y轴于点E,
∵A(2,0),B(0,4),
∴OA=2,OB=4,
∵四边形ABCD是正方形,
∴∠ABC=90°,BC=BA,
∵∠ABO+∠A=90°,∠ABO+∠CBE=90°,
∴∠CBE=∠BAO,
在△ABO和△BCE中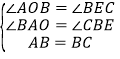 ,
,
∴△ABO≌△BCE(AAS),
∴BE=OA=2,CE=OB=4,
∴OE=OB﹣BE=4﹣2=2,
∴C点坐标为(﹣4,2).
故答案为:(﹣4,2).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目