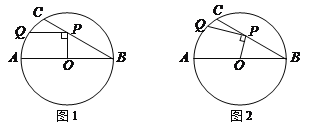题目内容
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠ABC的平分线BE交⊙O于点E,∠ACB的平分线CF交⊙O于点F,BE和CF相交于点D,四边形AFDE是菱形吗?请证明你的结论.

【答案】四边形AFDE是菱形.证明见解析.
【解析】试题分析:由AB=AC,BE平分∠ABC,CF平分∠ACB,可证∠ABE=∠EBC=∠ACF=∠FCB,再由圆周角定理的推论可证∠FAB=∠ABE=∠EAC=∠ACF.从而可证四边形AFDE是平行四边形,再证AF=AE,即证四边形AFDE是菱形.
解:四边形AFDE是菱形.
证明:∵AB=AC,
∴∠ABC=∠ACB.
又∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠EBC=∠ACF=∠FCB.
∵∠FAB,∠FCB是同弧所对的圆周角,
∴∠FAB=∠FCB,
同理∠EAC=∠EBC.
∴∠FAB=∠ABE=∠EAC=∠ACF.
∴AF∥ED,AE∥FD,
∴四边形AFDE是平行四边形.
∵∠ABE=∠ACF,
∴![]() =
=![]() ,
,
∴AF=AE.
∴四边形AFDE是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目