Question

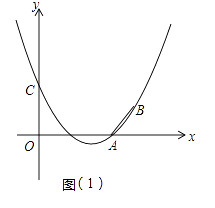
【题目】如图1，等边△ABC为⊙O的内接三角形，点G和点F在⊙O上且位于点A的两侧，连接BF、CG交于点E，且BF=CG．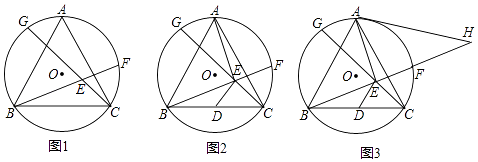

（1）求证：∠BEC=120°；
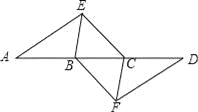
（2）如图2，取BC边中点D，连接AE、DE，求证：AE=2DE；
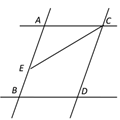
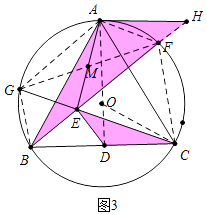
（3）如图3，在（2）的条件下，过点A作⊙O的切线交BF的延长线于点H，若AE=AH=4，请求出⊙O的半径长．

Answer 1

【答案】
（1）证明：如图1中，

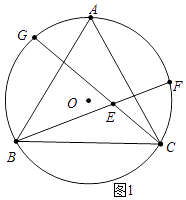
∵BF=CG，

∴ =

∵△ABC是等边三角形，

∴AC=BC，∠ACB=60°，

∴ = ，

∴ = ，

∴∠ACG=∠CBF，

∵∠GEB=∠FBC+∠ECB=∠ACE+∠ECB=60°，

∴∠BEC=180°﹣∠GEB=120°．

（2）证明：如图2中，连接BG、AG、CF、AF、GF，GF与AE交于点M．

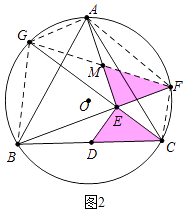
∵∠BEC=120°，

∴∠FEC=∠GEB=60°，

∵∠BGE=∠BAC=60°，∠EFC=∠BAC=60°，

∴△BGE，△EFC都是等边三角形，

∵∠AFB=∠ACB=60°，

∴∠GEB=∠AFB=60°，

∴GE∥AF，同理BF∥AG，

∴四边形AGEF是平行四边形，

∴GM=MF，AM=ME，

∵∠GBF=∠BAC=60°，

∴ = ，

∵BD=CD，

∴MF=CD，

在△MFE和△DCE中，

，

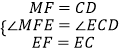∴△MFE≌△DCE，

∴ME=DE，

∴AE=2DE．

（3）解：如图3中，在图（2）的基础上连接OC．

由（2）可知，△MFE≌△DCE，

∴∠FEM=∠CED，

∵AH=AE=4，

∴∠H=∠AEH，DE=2，

∴∠H=∠CED，

∵BG=GE=AF，

∴ = ，

∴∠ECD=∠ABH，

∴△AHB∽△DEC，

∴ = =2，设BE=x，EC=EF=y，BD=a，

∴BH=2EC，

∴FH=y﹣x，

∵∠HAF=∠ABH，∠H=∠H，

∴△HAF∽△HBA，

∴AH2=HFHB，

∴16=2y（y﹣x） ①

∵BD=CD，∴AD⊥BC，AD经过点O，

∵AH是切线，

∴AH⊥AD，

∴AH∥BC，

∴∠H=∠CBE，

∴∠CED=∠CBE，∵∠ECD=∠ECB，

∴△ECD∽△BCE，

∴EC2=CDCB，

∴y2=a2a，

∴a= y，

∵ = ，

∴ = ，

∴x=2 代入①中解得y= + （负根已经舍弃），

∴CD=a= （ + ）=1+ ，

在Rt△COD中，∵∠OCD=30°，

∴cos30°= ，

∴OC=

【解析】（1）利用“同圆中，等弦所对的劣弧相等”，得出∠GEB=∠FBC+∠ECB=∠ACE+∠ECB=60°，可求出∠BEC度数；（2）通过“连接BG、AG、CF、AF、GF，GF与AE交于点M“构造出四边形AGEF，利用等弧所对的圆周角相等，可证出四边形AGEF是平行四边形，进而证得△MFE≌△DCE，ME=DE，AE=2DE；（3）可证出△AHB∽△DEC，△HAF∽△HBA，得出AH2=HFHB，求出y与a 的关系，再由AH是切线，证出△ECD∽△BCE，对应边成比例，求出x,再利用30度角的余弦，得出OC与CD的关系，求出OC.