��Ŀ����
����Ŀ���ۺ���ʵ�� �����龳��
�ۺ���ʵ�����ϣ�ͬѧ���ԡ�������ֽƬ���۵�����ת��Ϊ����չ����ѧ���̽���йص���ѧ���⣮
���ֲ�����
��֪��������ֽƬ![]() �У�
�У�![]() .��������ֽƬ
.��������ֽƬ![]() �����²�����в�����
�����²�����в�����
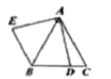
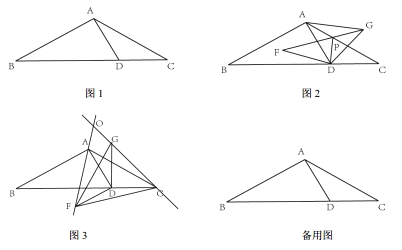
��һ������ͼ1���۵�������ֽƬ![]() ��ʹ��
��ʹ��![]() ���
���![]() �غϣ�Ȼ��չ����ƽ���ۺ۷ֱ�
�غϣ�Ȼ��չ����ƽ���ۺ۷ֱ�![]() �ڵ�
�ڵ�![]() ������
������![]() ����֪
����֪![]() ��
��
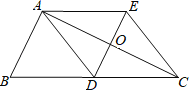
�ڶ�������ͼ1�Ļ����ϣ���������ֽƬ![]() ��
��![]() �������õ�
�������õ�![]() ��
��![]() .����
.����![]() ��λ�ò��䣬��
��λ�ò��䣬��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת�õ�
��ʱ����ת�õ�![]() (��
(��![]() �ֱ���
�ֱ���![]() �Ķ�Ӧ��)����ת��Ϊ
�Ķ�Ӧ��)����ת��Ϊ![]() ��������
��������
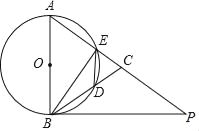
��1����ͼ2��С������ת��![]() ʱ��ͼ�Σ����߶�
ʱ��ͼ�Σ����߶�![]() ���ڵ�
���ڵ�![]() ������
������![]() .����
.С����![]() ����ֱ��ʼ�մ�ֱƽ���߶�
����ֱ��ʼ�մ�ֱƽ���߶�![]() .��֤����һ���ۣ�
.��֤����һ���ۣ�
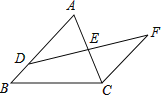
��2����ͼ3��Сӱ��������ת��![]() ʱ��ͼ�Σ���ֱ��
ʱ��ͼ�Σ���ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() �жϴ�ʱ
�жϴ�ʱ![]() ����״��˵�����ɣ�
����״��˵�����ɣ�
��3����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת�����У���
��ʱ����ת�����У���![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �����ľ��룮
�����ľ��룮
���𰸡���1������⣻��2����COFΪ�ȱ������Σ�֤������⣻��3��![]() ��
��![]() ��
��
��������
��1��������ת�á�ADC�ա�FDG���ɵö�Ӧ�߶�Ӧ�Ƿֱ���ȣ��Ӷ�ת��֤��FDM�ա�CDN����һ���ĵ�MD=ND����֤��AM=GN���ɴ˿�֤��APM�ա�GPN��������ô�ֱƽ���ߵ��ж����ɣ�
��2���ɵڣ�1�����еĽ��۽��90��ǿ��Լ���õ���OFC=��OCF=60�㣬�Ӷ���֤��
��3������Ҫ�������������ͼ�Σ��ٽ������ɶ���������Ŀ������֪�������㼴�ɣ�
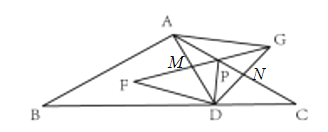
��1��֤��������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת�õ�
��ʱ����ת�õ�![]()
���ADC�ա�FDG
��AD=FD, DG=DC, ��DAC=��DFG����C=��DGF����ADC=��FDG��
��AD=DC
���DAC=��C��DA=DF=DC=DG��
���DAC=��DFG=��C=��DGF��
�ߡ�ADC=��FDG��
����FDM=��CDN��
�ڡ�FDM����CDN��
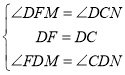
���FDM�ա�CDN(ASA)
��MD=ND,
��MA=NG,
�ڡ�APM����GPN��
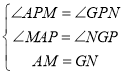
���APM�ա�GPN (AAS)
��PA=PG
����DA=DG
��DP��ֱƽ��AG��
��2���⣺��COFΪ�ȱ������Σ�
�������£�����ת��![]()
����FDA=��GDC=90��
����DF=DA,DG=DC
����DFA=��DAF=��DGC=��DCG=45��
��![]()
����B=��DCA=30��
��AD=DC
����DAC=��DCA=30��
����ADC=120��
����FDC=360��-��ADC-��ADF=360��-120��-90��=150��
��DF=DC
����DFC=��DCF=15��
����OFC=��DFC+��DFA=45��+15��=60��
��OCF=��DCG+��DCF=45��+15��=60��
����OFC=��OCF
��OC=OF
���ߡ�OCF=60��
���COFΪ�ȱ�������
��3���⣺��ͼ1���ߡ�BAC=120������DAC=30��
���BAD=90����
���ߡ�ABC=30����
��AD=![]() BD��
BD��
��CD=![]() BD��
BD��
��BC=6��
��CD=AD=2��BD=4
��FD=AD=2��
��![]() ����AFD=30����
����AFD=30����
��OD=![]() FD=1��OF=
FD=1��OF=![]() ,
,
��BO=BD-OD=4-1=3,
����Rt��BOF��BF=![]()
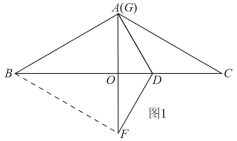
��ͼ2��BO=BD+OD=4+1=5,
����Rt��BOF��BF=![]()
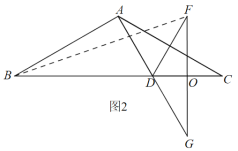
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���߲˻�����ֲ�����˺��Ͳ������߲˹�![]() Ķ������ֲ����
Ķ������ֲ����![]() Ķ��������Ϊ
Ķ��������Ϊ![]() ��Ԫ���й����ݼ��±���
��Ԫ���й����ݼ��±���
�ɱ�����λ����Ԫ/Ķ�� | ���۶��λ����Ԫ/Ķ�� | |
���� | 2.4 | 3 |
�Ͳ� | 2 | 2.5 |
��1����![]() ����
����![]() �ĺ�����ϵʽ������ = ���۶� �C �ɱ�����
�ĺ�����ϵʽ������ = ���۶� �C �ɱ�����
��2�����ƻ�Ͷ����ܳɱ�������![]() ��Ԫ��Ҫʹ��õ������������Ӧ��ֲ���˺��Ͳ˸�����Ķ��
��Ԫ��Ҫʹ��õ������������Ӧ��ֲ���˺��Ͳ˸�����Ķ��
��3����֪����ÿĶ����Ҫ����![]() kg���Ͳ�ÿĶ����Ҫ����
kg���Ͳ�ÿĶ����Ҫ����![]() kg�����ݣ�2���е���ֲĶ�������ؼƻ���������ȫ�����ʣ�Ϊ�����Ч�ʣ�ʵ��ÿ�����ͻ��ʵ�������ԭ�ƻ���
kg�����ݣ�2���е���ֲĶ�������ؼƻ���������ȫ�����ʣ�Ϊ�����Ч�ʣ�ʵ��ÿ�����ͻ��ʵ�������ԭ�ƻ���![]() �������������ȫ�����ʵĴ�����ԭ�ƻ���
�������������ȫ�����ʵĴ�����ԭ�ƻ���![]() �Σ������ԭ�ƻ�ÿ�����Ͷ��ٻ���.
�Σ������ԭ�ƻ�ÿ�����Ͷ��ٻ���.