题目内容
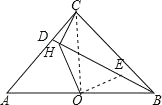
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .

【答案】![]() .
.
【解析】
试题分析:在BD上截取BE=CH,连接CO,OE,
∵∠ACB=90°CH⊥BD,
∵AC=BC=3,CD=1,
∴BD=![]() ,
,
∴△CDH∽△BDC,
∴![]() ,
,
∴CH=![]() ,
,
∵△ACB是等腰直角三角形,点O是AB中点,
∴AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,
∴∠OCH+∠DCH=45°,∠ABD+∠DBC=45°,
∵∠DCH=∠CBD,∴∠OCH=∠ABD,
在△CHO与△BEO中,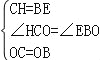 ,
,
∴△CHO≌△BEO,
∴OE=OH,∠BOE=∠HOC,
∵OC⊥BO,
∴∠EOH=90°,
即△HOE是等腰直角三角形,
∵EH=BD﹣DH﹣CH=![]() ﹣
﹣![]() ﹣
﹣![]() =
=![]() ,
,
∴OH=EH×![]() =
=![]() ,
,

练习册系列答案
相关题目