题目内容
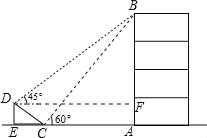
【题目】如图，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．
（1）求斜坡CD的高度DE；
（2）求大楼AB的高度（结果保留根号）
【答案】（1）2米；（2）（6+）或（6-）米.
【解析】
试题分析：（1）在在Rt△DCE中，利用30°所对直角边等于斜边的一半，可求出DE=2米；（2）过点D作DF⊥AB于点F，则AF=2，根据三角函数可用BF表示BC、BD，然后可判断△BCD是Rt△，进而利用勾股定理可求得BF的长，AB的高度也可求.
试题解析：（1）在Rt△DCE中，∠DEC=90°，∠DCE=30°，∴DE=DC=2米；（2）过D作DF⊥AB，交AB于点F，则AF=DE=2米.∵∠BFD=90°，∠BDF=45°，∴∠BFD=45°，∴BF=DF.设BF=DF=x米，则AB=（x+2）米，在Rt△ABC中，∠BAC=90°，∠BCA=60°，∴sin∠BCA=，∴BC=AB÷sin∠BCA=（x+2）÷
=
米，在Rt△BDF中，∠BFD=90°，
米，∵∠DCE=30°，∠ACB=60°，∴∠DCB=90°.∴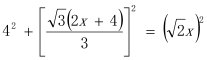
，解得：x=4+或x=4﹣，则AB=（6+）米或（6﹣）米．
练习册系列答案
相关题目
