��Ŀ����
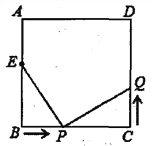
����Ŀ����ͼ����֪������ABCD�У��߳�Ϊ10cm����E��AB���ϣ�BE��6cm�������P���߶�BC����4cm/����ٶ���B����C���˶���ͬʱ����Q���߶�CD����acm/����ٶ���C����D���˶������˶���ʱ��Ϊt�룬
��1��CP�ij�Ϊ cm���ú�t�Ĵ���ʽ��ʾ����
��2������E��B��PΪ����������κ���P��C��QΪ�����������ȫ�ȣ���a��ֵ��
��3������Q�ԣ�2���е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ����������ABCD�ı��˶������P���Q���������������������˵�����ɣ�����������������ʱ���P���Q��һ����������ABCD�ĺδ�������
���𰸡���1��10-4t ����2��a��ֵΪ4��4.8����3������37.5�룬P��Q��һ���������ε�A������.
�������������������1��������ɵ�BP=4t���Ӷ��ɵ�CP�ij���
��2����������ۡ�BPE���PCQȫ�ȣ�ͨ����ͬ�Ķ�Ӧ��ϵ������ã�
��3����������ۣ�����ٶ�һ������������ֻ�в�ͬ���ٶȲſ������������ͨ����2����a�IJ�ֵͬ�������ۼ��ɵ�.
�����������1��PC=BC-BP=10-4t ��
��2������BEP�ա�CPQʱ��BE=CP��BP=CQ����6=10-4t��4t=at����t=1,a=4��
����BEP�ա�CQPʱ��BP=CP��BE=CQ����10-4t=4t��6=at����t=1.25��a=4.8��
��a��ֵΪ4��4.8��
��3����a=4ʱ��P��Q���˶��ٶ���ͬ���˶�����һ�£���P��Q����������
��a=4.8ʱ���辭��x���P��Q��һ��������
4.8x-4x=30��
x=37.5��
������37.5�룬P��Q��һ���������ε�A������.