��Ŀ����
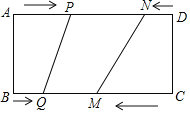
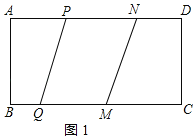
����Ŀ����ͼ���ھ���ABCD�У�BC��20cm��P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ھ��εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ��ֹͣ����֪����ͬʱ���ڣ���BQ��xcm��x��0������AP��2xcm��CM��3xcm��DN��x2cm��
����xΪ��ֵʱ��AP��ND������ȣ�
����xΪ��ֵʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�
����xΪ��ֵʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
���𰸡�����xΪ2ʱ��AP��ND������ȣ�����xΪ![]() ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�����x��2��x��4ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�����x��2��x��4ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
��������
(��)������ó����̣��ⷽ�̼��ɣ�
(��)����P���N�غϻ��Q���M�غ����������������ó����̣��ⷽ�̼��ɣ�
(��) ��P��N���������������ۣ���P�ڵ�N�������P�ڵ�N���Ҳ࣬��һ������ƽ���ı��ε������������̽�ɣ�
(��)��![]() ��
��
��AP=NDʱ����![]() ��
��
��ã�![]() ��
��![]() (��ȥ)��
(��ȥ)��
�൱![]() Ϊ2ʱ��AP��ND������ȣ�
Ϊ2ʱ��AP��ND������ȣ�
(��)����P���N�غϻ��Q���M�غ�ʱ����PQ��MNΪ���ߣ��Ծ��εı�(AD��BC)��һ����Ϊ�����߿��ܹ���һ�������Σ�
������P���N�غ�ʱ��
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��
��![]() ����ʱ��Q���M���غϣ�
����ʱ��Q���M���غϣ�
��![]() �������⣻
�������⣻
������Q���M�غ�ʱ��
������ã�![]() ��
��
��ã�![]() ��
��
��ʱ![]() �����������⣬
�����������⣬
���Q���M�����غϣ�
��������������![]() ��ֵΪ��
��ֵΪ��![]() ��
��
(��)�ߵ�N�㵽��A��ʱ��![]() ����ʱM���Q�㻹δ������
����ʱM���Q�㻹δ������
���Qֻ���ڵ�M����࣬
������P�ڵ�N�����ʱ����ͼ1��ʾ��
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��![]() ��
��
��![]() ʱ�ı���PQMN��ƽ���ı��Σ�
ʱ�ı���PQMN��ƽ���ı��Σ�
������P�ڵ�N���Ҳ�ʱ����ͼ2��ʾ��
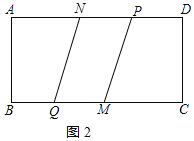
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��![]() ��
��
��![]() ʱ���ı���NQMP��ƽ���ı��Σ�
ʱ���ı���NQMP��ƽ���ı��Σ�
������������![]() ��
��![]() ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�

����Ŀ������ͼ�У�ÿ���������б߳�Ϊ1 ��С��������ɣ�
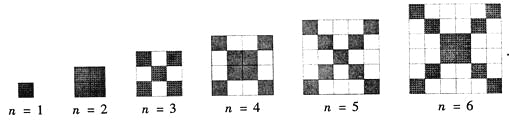
��1�� �۲�ͼ�Σ�����д���б���
�����α߳� | 1 | 3 | 5 | 7 | �� | n(����) |
��ɫС�����θ��� | �� | |||||
�����α߳� | 2 | 4 | 6 | 8 | �� | n(ż��) |
��ɫС�����θ��� | �� |
��2���ڱ߳�Ϊn��n��1�����������У����ɫС�����εĸ���ΪP1����ɫС�����εĸ���ΪP2�����Ƿ����ż��n��ʹP2��5P1�������ڣ���д��n��ֵ���������ڣ���˵������.