题目内容
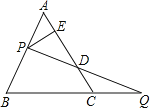
【题目】如图,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
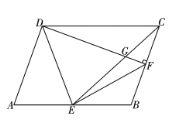
(1)四边形![]() 是平行四边形吗?说明理由;
是平行四边形吗?说明理由;
(2)求证:![]() ;
;
(3)若点![]() 是
是![]() 边的中点,求证:
边的中点,求证:![]() .
.
【答案】(1)四边形![]() 是平行四边形,理由见解析;(2)见解析;(3)见解析
是平行四边形,理由见解析;(2)见解析;(3)见解析
【解析】
(1)由![]() 可得AB∥DC,再由AB=DC即可判定四边形ABCD为平行四边形;
可得AB∥DC,再由AB=DC即可判定四边形ABCD为平行四边形;
(2)由AB∥DC可得∠AED=∠CDE,然后根据CE=AB=DC可得∠CDE=∠CED,再利用三角形内角和定理即可推出∠AED与∠DCE的关系;
(3)延长DA,FE交于点M,由“AAS”可证△AEM≌△BEF,可得ME=EF,由直角三角形的性质可得DE=EF=ME,由等腰三角形的性质和外角性质可得结论.
(1)四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
∵![]()
∴AB∥DC
又∵AB=DC
∴四边形![]() 是平行四边形.
是平行四边形.
(2)∵AB∥DC
∴∠AED=∠CDE
又∵AB=DC,CE=AB
∴DC=CE
∴∠CDE=∠CED
∴在△CDE中,2∠CDE+∠DCE=180°
∴∠CDE=90°-![]() ∠DCE
∠DCE
∴![]()
(3)如图,延长DA,FE交于点M,
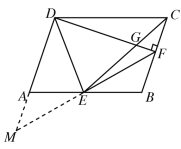
∵四边形ABCD为平行四边形
∴DM∥BC,DF⊥BC
∴∠M=∠EFB,DF⊥DM
∵E为AB的中点
∴AE=BE
在△AEM和△BEF中,
∵∠M=∠EFB,∠AEM=∠BEF,AE=BE
∴△AEM≌△BEF(AAS)
∴ME=EF
∴在Rt△DMF中,DE为斜边MF上的中线
∴DE=ME=EF
∴∠M=∠MDE,
∴∠DEF=∠M+∠MDE=2∠M=2∠EFB.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
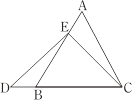
激活思维智能训练课时导学练系列答案【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
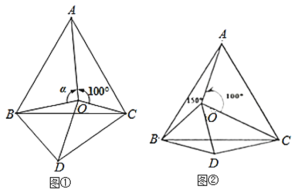
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).