题目内容
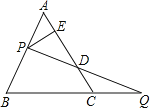
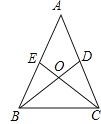
【题目】如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
A.2种B.3种C.4种D.6种
【答案】C
【解析】
①②:求出OBC=∠OCB,推出∠ACB=∠ABC即可的等腰三角形;①③:证△EBO≌△DCO,得出∠EBO=∠DCO,求出∠ACB=∠ABC即可;②④:证△EBO≌△DCO,推出OB=OC,求出∠ABC=∠ACB即可;③④:证△EBO≌△DCO,推出∠EBO=∠DCO,OB=OC,求出∠OBC=∠OCB,推出∠ACB=∠ABC即可.
解:有①②,①③,②④,③④,共4种,
①②,
理由是:∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形;
①③,
理由是:∵在△EBO和△DCO中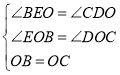 ,
,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,
∵∠OBC=∠OCB(已证),
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
②④,
理由是:∵在△EBO和△DCO中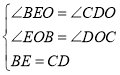 ,
,
∴△EBO≌△DCO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
③④,
理由是:∵在△EBO和△DCO中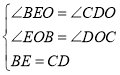 ,
,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
故选C.