题目内容
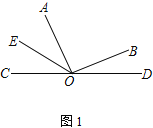
【题目】已知O是直线上的一点,∠AOB是直角,OE平分∠AOC
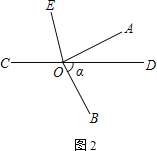
(1) 在图①中,若∠BOD=28°,求∠AOE的度数
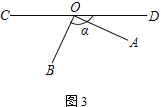
(2) 将图①中的∠AOB绕顶点O顺时针旋转至图②的位置.若∠BOD=α,试用含α的式子表示∠AOE,并说明理由
(3) 继续旋转AOB至图③的位置,若∠BOD=α,其他条件不变,试将图形补充完整,求∠AOE的度数.(用含α的式子表示)
【答案】(1)∠AOE=31°;(2)∠AOE=45°+![]() α,理由见解析;(3)作图见解析,∠AOE=135°-
α,理由见解析;(3)作图见解析,∠AOE=135°-![]() α.
α.
【解析】
(1)求出∠AOC,根据角平分线定义求出∠AOE,即可求出答案;
(2)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
(3)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
解:(1)∵∠AOB是直角,∠BOD=28°,
∴∠AOC=180°-∠AOB-∠BOD=180°-90°-28°=62°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×62°=31°;
×62°=31°;
(2)∠AOE=45°+![]() α,理由如下:
α,理由如下:
∵∠AOB是直角,∠BOD=α,
∴∠AOD=90°-α,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(90°-α)= 90°+α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(90°+α)=45°+
×(90°+α)=45°+![]() α;
α;
(3)如图,
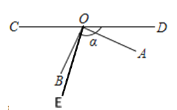
∵∠AOB是直角,∠BOD=α,
∴∠AOD=α-90°,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(α-90°)= 270°-α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(270°-α)=135°-
×(270°-α)=135°-![]() α.
α.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目