题目内容
【题目】如图,直线y=﹣x+b与反比例函数y= ![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB. 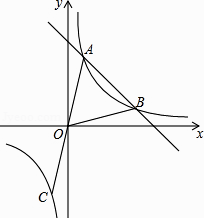
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使S△PAC= ![]() S△AOB?若存在请求出点P坐标,若不存在请说明理由.
S△AOB?若存在请求出点P坐标,若不存在请说明理由.
【答案】
(1)解:将A(1,4)分别代入y=﹣x+b和 ![]()
得:4=﹣1+b,4= ![]() ,解得:b=5,k=4
,解得:b=5,k=4
(2)解:一次函数值小于反比例函数值的自变量x的取值范围为:x>4或0<x<1
(3)解:过A作AN⊥x轴,过B作BM⊥x轴,
由(1)知,b=5,k=4,
∴直线的表达式为:y=﹣x+5,反比例函数的表达式为: ![]()
由 ![]() ,解得:x=4,或x=1,
,解得:x=4,或x=1,
∴B(4,1),
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),
∴S△PAC= ![]() OPCD+
OPCD+ ![]() OPAE=
OPAE= ![]() OP(CD+AE)=|t|=3,
OP(CD+AE)=|t|=3,
解得:t=3,t=﹣3,
∴P(0,3)或P(0,﹣3).
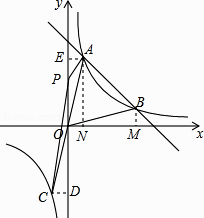
【解析】(1)由待定系数法即可得到结论;(2)根据图象中的信息即可得到结论;(3)过A作AM⊥x轴,过B作BN⊥x轴,由(1)知,b=5,k=4,得到直线的表达式为:y=﹣x+5,反比例函数的表达式为: ![]() 列方程
列方程 ![]() ,求得B(4,1),于是得到
,求得B(4,1),于是得到 ![]() ,由已知条件得到
,由已知条件得到 ![]() ,过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),根据三角形的面积公式列方程即可得到结论.
,过A作AE⊥y轴,过C作CD⊥y轴,设P(0,t),根据三角形的面积公式列方程即可得到结论.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正常字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题: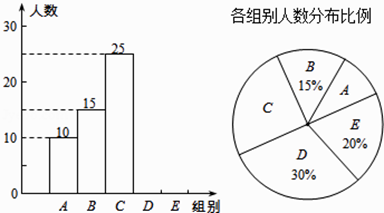
(1)统计表中的m= , n= , 并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.