题目内容
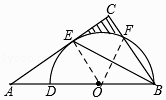
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 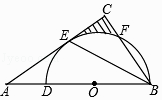
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
【答案】
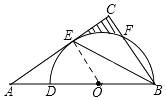
(1)解:连接OE,
∴BE是∠OBC的角平分线,
∴∠OBE=∠CBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∵OE是⊙O的半径,
∴AC是⊙O的切线;
(2)解:连接OF,
∵cosA= ![]() ,
,
∴∠A=30°,
∴∠ABC=∠AOE=60°
∵OB=OF=3,
∴∠FOB=∠ABC=60°,
∴∠EOF=60°,
∴扇形OEF的面积为: ![]() =
= ![]() ,
,
∵OE=3,∠BAC=30°,
∴AO=2OE=6,
∴AB=AO+OB=9,
∴BC= ![]() AB=
AB= ![]()
∴由勾股定理可知:AE=3 ![]() ,AC=
,AC= ![]() ,
,
∴CE=AC﹣AE= ![]() ,
,
∵BF=OB=3,
∴CF=BC﹣BF= ![]()
∴梯形OFCE的面积为: ![]() =
= ![]() ,
,
∴阴影部分面积为: ![]() ﹣
﹣ ![]()
【解析】(1)连接,根据BE平分∠OBC,OE=OB,可得出OE∥BC,从而可知∠AEO=∠C=90°,根据切线的判定,即可得出AC是⊙O的切线;(2)连接OF,根据条件分别求出OE、CF、CE,∠EOF的数值后,根据面积公式分别计算梯形OFCE与扇形EOF的面积,从而可求出阴影部分的面积.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11 815元.已知两种球厂家的批发价和商场的零售价如右表,试解答下列问题:
品名 | 厂家批发价(元/只) | 市场零售价(元/只) |
篮球 | 130 | 160 |
排球 | 100 | 120 |
(1)该采购员最多可购进篮球多少只?
(2)若该商场把这100只球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少只,该商场最多可盈利多少元?