题目内容
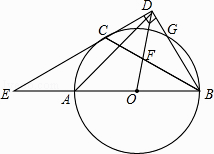
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
【答案】
(1)证明:连接OC,
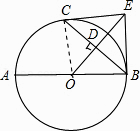
∵OD⊥BC,
∴∠COE=∠BOE,
在△OCE和△OBE中,
∵ 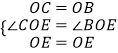 ,
,
∴△OCE≌△OBE,
∴∠OBE=∠OCE=90°,即OB⊥BE,
∵OB是⊙O半径,
∴BE与⊙O相切.
(2)解:过点D作DH⊥AB,连接AD并延长交BE于点F,
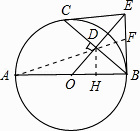
∵∠DOH=∠BOD,∠DHO=∠BDO=90°,
∴△ODH∽△OBD,
∴ ![]() =
= ![]() =
= ![]()
又∵sin∠ABC= ![]() ,OB=9,
,OB=9,
∴OD=6,
易得∠ABC=∠ODH,
∴sin∠ODH= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴OH=4,
∴DH= ![]() =2
=2 ![]() ,
,
又∵△ADH∽△AFB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴FB= ![]()
【解析】(1)连接OC,先证明△OCE≌△OBE,得出EB⊥OB,从而可证得结论.(2)过点D作DH⊥AB,根据sin∠ABC= ![]() ,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.
,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.

练习册系列答案
相关题目