题目内容
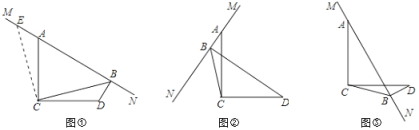
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.
(1)问题发现
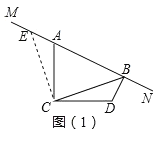
如图①过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为 ;BD、AB、CB之间的数量关系为 .
(2)拓展探究
当MN绕点A旋转到如图②位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并证明.
(3)解决问题
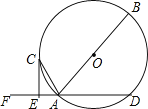
当MN绕点A旋转到如图③位置时(点C,D在直线MN两侧),若此时∠BCD=30°,BD=2,则CB= .
【答案】(1)BD=AE,![]() ;(2)
;(2)![]() ,见解析;(3)
,见解析;(3)![]()
【解析】
(1)过点C作CE⊥CB,得到∠BCD=∠ACE,判断出△ACE≌△DCB,确定△ECB为等腰直角三角形即可.
(2)过点C作CE⊥CB于点C,判断出△ACE≌△DCB,确定△ECB为等腰直角三角形,即可得出结论;
(3)先判断出△ACE≌△BCD,CE=BC,得到△BCE为等腰直角三角形,得到![]() ,求出BH,再用勾股定理即可.
,求出BH,再用勾股定理即可.
解:(1)如图1,过点C作⊥CB交MN于点E,
∵∠ACD=90°,
∴∠ACE=90°-∠ACB,∠BCD=90°-∠ACB,
∴∠ACE=∠BCD,
∵DB⊥MN,
∴在四边形ACDB中,∠BAC+∠ACD+∠ABD+∠D=360°,
∴∠BAC+∠D=180°,
∵∠CAE+∠BAC=180°,
∠CAE=∠D,
∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∵∠ECB=90°,
∴△ECB是等腰直角三角形,
![]() ,
,
∴BE=AE+AB=DB+AB,
![]() ,
,
故答案为:BD=AE,![]() ;
;
(2)如图2,过点C作⊥CB交MN于点E,
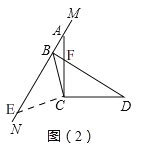
∵∠ACD=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠ACE=∠BCD,
∵DB⊥MN,
∴∠CAE=90°-∠AFB,∠D=90°-∠CFD,
∵∠AFB=∠CFD,
∴∠CAE=∠D,
∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∵∠ECB=90°,
∴△ECB是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ;
;
(3)如图3,过点C作⊥CB交MN于点E,
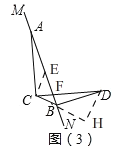
∵∠ACD=90°,
∴∠ACE=90°-∠DCE,
∠BCD=90°-∠DCE,
∴∠ACE=∠BCD,
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠CFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∵∠ECB=90°,
∴△ECB是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
∵△BCE为等腰直角三角形,
∴∠BEC=∠CBE=45°,
∵∠ABD=90°,
∴∠DBH=45°
过点D作DH⊥BC,
∴△DHB是等腰直角三角形,
![]() ,
,
![]() ,
,
在Rt△CDH中,![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() .
.

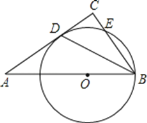
【题目】如图:在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E。
(1)试说明:AC是⊙O的切线;
(2)若BC=6,tan∠A=![]() ,求⊙O的半径。
,求⊙O的半径。