Question

【题目】如图，矩形ABCD，AD＝1，CD＝2，点P为边CD上的动点（P不与C重合），作点P关于BC的对称点Q，连结AP，BP和BQ，现有两个结论：①若DP≥1，当△APB为等腰三角形时，△APB和△PBQ一定相似；②记经过P，Q，A三点的圆面积为S，则4π≤S＜．

下列说法正确的是（　　）

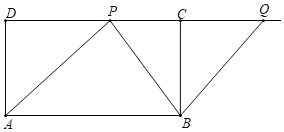
A. ①对②对B. ①对②错C. ①错②对D. ①错②错

Answer 1

【答案】A

【解析】

①在Rt△ADP中，由AP＝2AD，推出∠APD＝30°，即可解决问题．

②求出两种特殊位置的⊙O的面积即可判断．

①如图1中，

∵DP≥1，当△APB为等腰三角形，

∴只有AP＝AB，

在Rt△ADP中，∵∠D＝90°，AP＝2，AD＝1，

∴PA＝2AD，

∴∠APD＝30°，

∵CD∥AB，

∴∠CPB＝∠ABP，

∵AP＝AB，

∴∠ABP＝∠APB，

∴∠APB＝∠CPB＝75°，

∵P，Q关于BC对称，

∴BP＝BQ，

∴∠BPC＝∠BQC＝75°，

∴△APB∽△BPQ，故①正确．

②如图2中，作△APQ的外接圆⊙O．

当点O与B重合时，⊙O的半径最小，此时⊙O的面积为4π，

当点P与C重合时，设OA＝OP＝x，

在Rt△AOB中，则有x2＝22+（x﹣1）2，

∴x＝，

此时⊙O的面积＝π，

观察图象可知：4π≤S＜π．故②正确，

故选：A．