题目内容
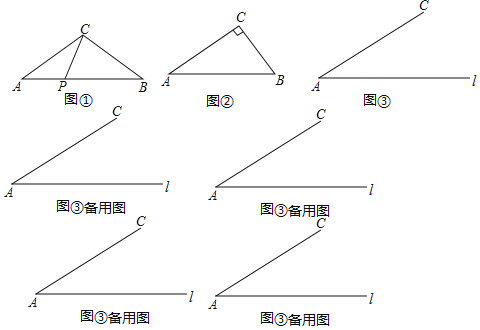
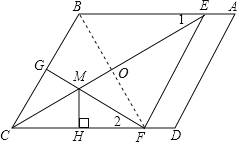
【题目】如图,在平行四边形ABCD中,CE平分∠BCD,交AB边于点E,EF∥BC,交CD于点F,点G是BC边的中点,连接GF,且∠1=∠2,CE与GF交于点M,过点M作MH⊥CD于点H.
(1)求证:四边形BCFE是菱形;
(2)若CH=1,求BC的长;
(3)求证:EM=FG+MH.

【答案】(1)见解析;(2)2;(3)见解析.
【解析】
(1)由在平行四边形ABCD中,EF∥BC,可得四边形BCFE是平行四边形,又由CE平分∠BCD,易得△BCE是等腰三角形,继而证得四边形BCFE是菱形;
(2)由∠1=∠2,可得∠ECF=∠2,即△CMF是等腰三角形,又由MH⊥CD,可得CF=2CH,继而求得BC的长;
(3)首先连接BC交CF于点O,易得△BCF是等边三角形,继而可得OM=MH,OE=FG,则可证得结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠ECF,
∵EF∥BC,
∴四边形BCFE是平行四边形,
∵CE平分∠BCD,
∴∠BCE=∠ECF,
∴∠BCE=∠1,
∴BC=BE,
∴四边形BCFE是菱形;
(2)∵∠1=∠ECF,∠1=∠2,
∴∠ECF=∠2,
∴CM=FM,
∵MH⊥CD,
∴CF=2CH=2×1=2,
∵四边形BCFE是菱形;
∴BC=CF=2;
(3)连接BF交CE于点O,
∵G是BC中点,
∴![]()
∵![]()
∴CG=CH,
在△CGM和△CHM中,
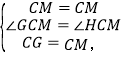
∴△CGM≌△CHM(SAS),
∴![]()
即FG⊥BC,
∴CF=BF,
∵BC=CF,
∴BC=CF=BF,
∴△BCF是等边三角形,
∴![]()
∴![]()
∵BF⊥CE,
∴OM=MH,
∵OE=OC=FG,
∴EM=FG+MH.

练习册系列答案
相关题目