Question

【题目】（题文）如图，在平面直角坐标系中，矩形OABC的顶点A（6，0），C（0，2），过y轴上的点D（0，3），作射线DM与x轴平行，点P，Q分别是射线DM与x轴正半轴上的动点，满足∠PQO=60°．设点P的横坐标为x（0≤x≤9），△OPQ与矩形的重叠部分的面积为y，则能大致反映y与x函数关系的图象是（　　）

A. B. C. D.

Answer 1

【答案】C

【解析】

根据选项时间，探究临界点前后的图形变化，分类讨论．分别采用相似三角形知识表示相应线段即可．

由已知当t=3时，点Q与点A重合，

由题意OD=3，∠PQO=60°，

当0≤t≤3时，

∵DM与x轴平行，

∴△PEF∽△POQ，

∴ ，

∴EF=，

∴y=（EF+OQ）CO=，

则选项A、D排除，

当t=5时，PQ过点B，当t=9时，点P过点B，

∴当5≤t≤9时，如图，

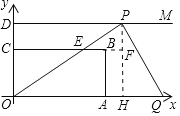
过点P作PH⊥OQ于点H，延长CB交PH于点F，

由已知，HQ=3，

则OH=x-3，

∵CB∥OQ，

∴△PEF∽△POH，

∴EF=x，

∴EB=x(x6)＝x+6，

∴y= (EB+OA)AB= (x+6+6)2＝ x+12，

此时y是x的一次函数，

∴选项D排除，

故选C．