Question

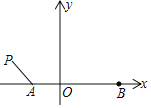
【题目】如图，在平面直角坐标系中，点A的坐标为（﹣1，0），点B的坐标为（2，0），点P为线段AB外一动点且PA＝1，以PB为边作等边△PBM，则当线段AM的长取到最大值时，点P的横坐标为_____．

Answer 1

【答案】﹣

【解析】

如图，将△MPA绕点P顺时针旋转60°，得到△BPN，连接AN．根据旋转不变性可知：PA＝PN，∠MPB＝∠APN＝60°，AM＝BN，推出△PAN是等边三角形，推出AN＝PA＝1，由BN≤AN+AB，推出当N，A，B共线时，BN的值最大，此时点N在BA的延长线上，由此即可解决问题.

如图，将△MPA绕点P顺时针旋转60°，得到△BPN，连接AN．

根据旋转不变性可知：PA＝PN，∠MPB＝∠APN＝60°，AM＝BN，

∴△PAN是等边三角形，

∴AN＝PA＝1，

∵BN≤AN+AB，

∴当N，A，B共线时，BN的值最大，此时点N在BA的延长线上，可得点P的横坐标为﹣1﹣，

故答案为：﹣．