题目内容
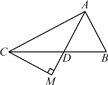
【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为 . 
【答案】(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() )
)
【解析】解:连接EC. 
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△ACE中, ,
,
∴△ABD≌△ACE,
∴BD=EC.∠ABD=∠ACE=45°,
∵∠ACB=45°,
∴∠ECD=90°,
∴点E在过点C垂直x轴的直线上,且EC=DB,①当DB=DA时,点D与O重合,BD=OB=2,此时E(2,2).②当AB=AD时,BD=CE=4,此时E(2,4).③当BD=AB=2 ![]() 时,E(2,2
时,E(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ),
),
故答案为(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ).
).
连接EC.只要证明△ABD≌△ACE,推出BD=EC.∠ABD=∠ACE=45°,由∠ACB=45°,推出∠ECD=90°,推出点E在过点C垂直x轴的直线上,且EC=DB,再分三种情形讨论即可解决问题.

【题目】如图是生活中常见的月历的示意图,请结合图示回答下列问题.
一 | 二 | 三 | 四 | 五 | 六 | 日 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)如图是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d分别与a的关系:b=________;c=________;d=________(用含a的代数式填空).
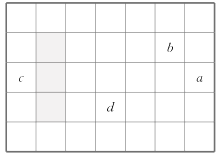
(2)用一个长方形框圈出月历中的三个数(如 图中的阴影),若这三个数之和等于51,则这三个数分别是多少?
(3)这样圈出的三个数的和可能是64吗?为什么?