题目内容
如图，四边形ABCD是边长为1 的正方形，四边形EFGH是边长为2的正方形，点D与点F重合，点B，D（F），H在同一条直线上，将正方形ABCD沿F→H方向平移至点B与点H重合时停止，设点D、F之间的距离为x，正方形ABCD与正方形EFGH重叠部分的面积为y，则能大致反映y与 x之间函数关系的图象是（ ）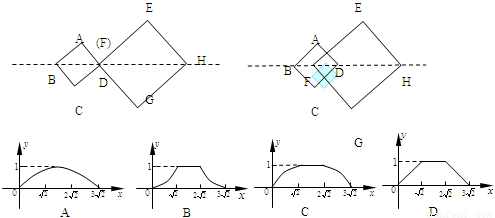
【答案】
B
【解析】
试题分析：重叠部分为正方形，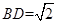
，当
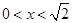时，此时，重叠部分面积为
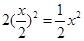，即函数图象为抛物线
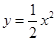中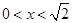时的图象，面积最大值1；为当
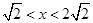，此时重叠面积固定，为小正方形面积，面积为1；当
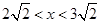，此时重叠部分面积为
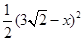，即函数图象为抛物线
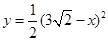中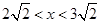时的图象，面积最小为0，综上，可以知道为B选项
考点：几何与函数的结合
点评：此题要观察函数的变化，可以用分段函数概括
练习册系列答案
相关题目
如图，四边形ABCD的对角线AC与BD互相垂直平分于点O，设AC=2a，BD=2b，请推导这个四边形的性质．（至少3条）
如图，四边形ABCD的对角线AC、BD交于点P，过点P作直线交AD于点E，交BC于点F．若PE=PF，且AP+AE=CP+CF．
如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数．
如图，四边形ABCD为正方形，E是BC的延长线上的一点，且AC=CE，求∠DAE的度数．