题目内容
如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°,点D在射线BC上运动时(与点B不重合),如图,线段CF,BD之间的位置关系为
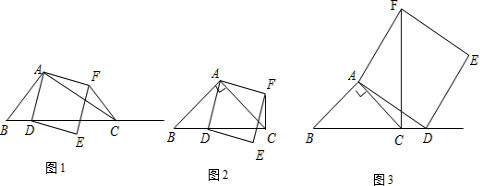
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且AC=4
| 2 |
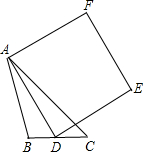
分析:(1)首先选择图2证明,由AB=AC,∠BAC=90°,可得:△ABC是等腰直角三角形,又由四边形ADEF是正方形,易证得△ABD≌△ACF(SAS),即可求得:CF=BD,∠ACF=∠B=45°,证得CF⊥BD;
(2)首先作辅助线:过点A作AG⊥BC,垂足为G,连接CF,易得:△AGD∽△DCP,由相似三角形的对应边成比例,即可求得:AG•CP=GD•DC,在等腰Rt△AGC中求得AC的值,设GD=x,即可求得CP关于x的二次函数,求得最大值.
(2)首先作辅助线:过点A作AG⊥BC,垂足为G,连接CF,易得:△AGD∽△DCP,由相似三角形的对应边成比例,即可求得:AG•CP=GD•DC,在等腰Rt△AGC中求得AC的值,设GD=x,即可求得CP关于x的二次函数,求得最大值.
解答:解:(1)CF⊥BD,CF=BD.
证明:选择图2证明:
∵AB=AC,∠BAC=90°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD+∠DAC=90°,∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中
,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B=45°,
∴∠BCF=90°,
∴CF⊥BD.
(2)如图,过点A作AG⊥BC,垂足为G,连接CF.
∴∠AGD=90°,
∴∠ADG+∠GAD=90°,
∵CF⊥BD.
∴∠PCD=90°,
∴∠PDC+∠DPC=90°,
∵∠ADE=90°,
∴∠ADG+∠PDC=90°,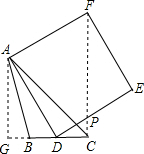
∴∠ADG=∠DPC,∠PDC=∠GAD,
∴△AGD∽△DCP,
∴
=
,
即AG•CP=GD•DC,
在等腰Rt△AGC中,
∵AC=4
,
∴AG=GC=4,
设GD=x,
则DC=4-x,
∵
=
,
∴
=
,
∴CP=
x(4-x),
∴CP=-
x2+x,
当x=2时,CP取得最大值,最大值为1.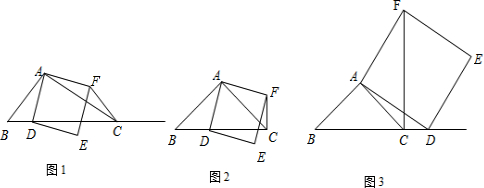
证明:选择图2证明:
∵AB=AC,∠BAC=90°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD+∠DAC=90°,∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中
|
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B=45°,
∴∠BCF=90°,
∴CF⊥BD.
(2)如图,过点A作AG⊥BC,垂足为G,连接CF.
∴∠AGD=90°,
∴∠ADG+∠GAD=90°,
∵CF⊥BD.
∴∠PCD=90°,
∴∠PDC+∠DPC=90°,
∵∠ADE=90°,
∴∠ADG+∠PDC=90°,

∴∠ADG=∠DPC,∠PDC=∠GAD,
∴△AGD∽△DCP,
∴
| AG |
| DC |
| GD |
| CP |
即AG•CP=GD•DC,
在等腰Rt△AGC中,
∵AC=4
| 2 |
∴AG=GC=4,
设GD=x,
则DC=4-x,
∵
| AG |
| DC |
| GD |
| CP |
∴
| 4 |
| 4-x |
| x |
| CP |
∴CP=
| 1 |
| 4 |
∴CP=-
| 1 |
| 4 |
当x=2时,CP取得最大值,最大值为1.

点评:此题考查了全等三角形与相似三角形的判定与性质,等腰直角三角形的性质以及二次函数最大值问题.此题综合性很强,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=