��Ŀ����
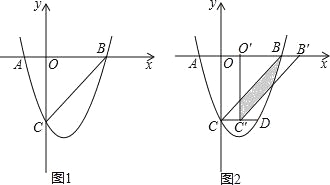
����Ŀ����ͼ��������y=ax2+bx+c��a��0����x�ᡢy��ֱ��ڵ�A����1��0����B��3��0����C��0����3�����㣮
��1��ֱ��д�������ߵĽ���ʽ ��
��2����D��2��m���ڵ�һ�����������ϣ�����BC��BD�����ʣ��ڶԳ����������������Ƿ����һ��P��������PBC=��DBC��������ڣ��������P������ꣻ��������ڣ���˵�����ɣ�
��3����ͼ2���ڣ�2���������£�����BOC��x����������ÿ��1����λ���ȵ��ٶ�����ƽ�ƣ���ƽ�ƺ��������Ϊ��B��O��C������ƽ�ƹ����У���B��O��C������BCD�ص��������ΪS����ƽ�Ƶ�ʱ��Ϊt�루0��t��3��������S��t֮��ĺ�����ϵʽ��
���𰸡�(1)��y=x2��2x��3;(2)��P����![]() ����
����![]() ����(3)��S=
����(3)��S= ��
��
��������
���������(1)�����������������߽���ʽ������ϵ�������ɵã�(2)�������D����ɵ�CD��x�ᣬ��B��C����ɵ���OCB=��CBO=��DCB=45�����̶�֤��CDB�ա�CQB�ɵ�CQ=CD=2������Q�����꣬�Ӷ����ֱ��BP�Ľ���ʽ�����������ϵĵ�P��n��n2��2n��3��������ֱ��BP����ʽ�����n��ֵ���ɵô𰸣�
(3)������C����CD���˶�ʱ����0��t��2ʱ�����ݣ�S=S��BCD��S��CC��E��S��C��DF����⼴�ɣ�����C����CD�ӳ������˶�ʱ����2��t��3ʱ�����ݣ�S=S��GEB�����ɵã�
���������(1)�����������������߽���ʽΪy=a��x+1����x��3����
����C��0����3�����룬�ã���3a=��3��
��ã�a=1�� ��y=��x+1����x��3��=x2��2x��3��
(2)�����ڣ� ����D��2��m�����������߽���ʽ�ã�m=��3�� ��D��2����3����
��B��3��0����C��0����3�� ��OC=OB�� ���OCB=��CBO=45���� ��ͼ1����BP��y���ڵ�Q��
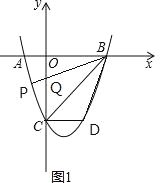
��CD��x�ᣬ ���DCB=��BCQ=45�� ���CDB�ա�CQB��ASA�� ��CQ=CD=2��
����Q��0����1���� ��ֱ��BP��y=kx��1��
��B��3��0������ã�3k��1=0�� ��k=![]() �� ��ֱ��BP��y=
�� ��ֱ��BP��y=![]() x��1��
x��1��
��P������Ϊ��n��n2��2n��3���� ����y=![]() x��1���ã�n2��2n��3=
x��1���ã�n2��2n��3=![]() n��1
n��1
��ã�n=��![]() ��n=3����ȥ�� ��n=��
��n=3����ȥ�� ��n=��![]() ʱ��n2��2n��3=��
ʱ��n2��2n��3=��![]() ��P����
��P����![]() ����
����![]() ����
����
(3)����B��3��0����C��0����3����D��2����3���� �����ֱ��BC��y=x��3��ֱ��BD��y=3x��9��
����0��t��2ʱ����ͼ2��
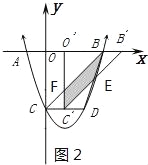
������֪��C����t����3����B����3+t��0�� �����ֱ��C��B����y=��x��t����3��������ֱ��BD��y=3x��9�����F��![]() ����
����![]() t���� �ߡ�DCB=45�� ��C��E=t
t���� �ߡ�DCB=45�� ��C��E=t
��S=S��BCD��S��CC��E��S��C��DF=![]() ��2��3��
��2��3��![]() ��t��t��
��t��t��![]() ����2��t����3��
����2��t����3��![]() t����
t����
�����ã�S=��![]() t2+3t��0��t��2��
t2+3t��0��t��2��
����2��t��3ʱ����ͼ3��
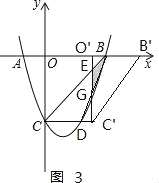
������֪��G��t��3t��9����E��t��t��3�� ��S=S��GEB=![]() [����3t+9��������t+3��]����3��t��
[����3t+9��������t+3��]����3��t��
�����ã�S=t2��6t+9��2��t��3���� ����������S= ��
��

 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�����Ŀ��ij����С����չ��Լ�õ�����С��100����ͥ4�·ݽڵ������ͼ��ʾ����ô���·���100����ͥ�Ľ�Լ��������λǧ��ʱ��ƽ�����ǣ�������
�ڵ�����ǧ��ʱ�� | 20 | 30 | 40 | 50 |
���������� | 20 | 30 | 30 | 20 |
A.35B.26C.25D.20

