��Ŀ����
����Ŀ������ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��5x��0��
�⣺��x2��5x=0����ã�x1=0��x2=5����������y=x2��5x��x��Ľ�������Ϊ��0��0���ͣ�5��0�����������κ���y=x2��5x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0����x��5ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��5x��0�����ԣ�һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��x��0��x��5��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1��������������У�����������ѧ˼���е��� �� ��ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼��
��2��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ ��
��3�������Ƶķ���д��һԪ���β���ʽ�Ľ⼯��x2��2x��3��0�� ��
���𰸡�
��1���٣���
��2��0��x��5
��3��x����1��x��3
���������⣺��1��������������У�����������ѧ˼���еĢٺۣ͢�
���Դ��ǣ��٣��ۣ���2����ͼ���֪����0��x��5ʱ����ͼ��λ��x���·���
��ʱy��0����x2��5x��0��
��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��0��x��5��
���Դ��ǣ�0��x��5����3����x2��2x��3=0��
��ã�x1=3��x2=��1��
��������y=x2��2x��3��x��Ľ�������Ϊ��3��0���ͣ���1��0����
�������κ���y=x2��2x��3�Ĵ���ͼ����ͼ��ʾ����
��ͼ���֪����x����1����x��3ʱ����ͼ��λ��x���Ϸ���
��ʱy��0����x2��2x��3��0��
��һԪ���β���ʽx2��2x��3��0�Ľ⼯Ϊ��x����1��x��3��
���Դ���x����1��x��3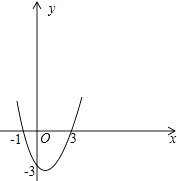
�����㾫����������������������Ľ������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�