题目内容
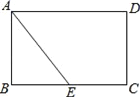
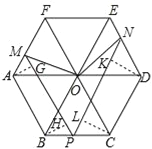
【题目】如图1,已知△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形,点P为边BC上任意一点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)那么∠MPN=______,并求证PM+PN=3a;
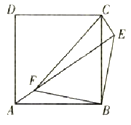
(2)如图2,联结OM、ON.求证:OM=ON;
(3)如图3,OG平分∠MON,判断四边形OMGN是否为特殊四边形,并说明理由.
【答案】60°;
【解析】(1)由∠MPN=180°﹣∠BPM﹣∠NPC即可得出∠MPN的度数;作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解;
(2)由SAS证明△OMA≌△ONE,得出对应边相等即可;
(3)由△OMA≌△ONE得出∠MOA=∠EON,再证出△GOE≌△NOD,得出OG=ON,由△ONG是等边三角形和△MOG是等边三角形即可得出四边形MONG是菱形.
(1)解:∵△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形
∴六边形ABCDEF是边长为a的正六边形,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°;
作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,如图所示:
MP+PN=MG+GH+HP+PL+LK+KN
∵正六边形ABCDEF中,PM∥AB,作PN∥CD,
∵∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM=![]() AM,HP=
AM,HP=![]() BP,PL=
BP,PL=![]() PC,NK=
PC,NK=![]() ND,
ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)证明:由(1)得:六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△OMA和△ONE中,
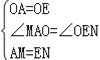 ,
,
∴△OMA≌△ONE(SAS)
∴OM=ON.
(3)解:四边形MONG是菱形;理由如下:
由(2)得,△OMA≌△ONE,
∴∠MOA=∠EON,
∵EF∥AO,AF∥OE,
∴四边形AOEF是平行四边形,
∴∠AFE=∠AOE=120°,
∴∠MON=120°,
∴∠GON=60°,
∵∠GOE=60°﹣∠EON,∠DON=60°﹣∠EON,
∴∠GOE=∠DON,
∵OD=OE,∠ODN=∠OEG,
在△GOE和△DON中,
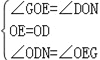 ,
,
∴△GOE≌△NOD(ASA),
∴OG=ON,
又∵∠GON=60°,
∴△ONG是等边三角形,
∴ON=NG,
又∵OM=ON,∠MOG=60°,
∴△MOG是等边三角形,
∴MG=GO=MO,
∴MO=ON=NG=MG,
∴四边形MONG是菱形.
“点睛”本题是四边形的综合题目,考查了等边三角形的性质与判定、全等三角形的判定与性质、正六边形的性质、平行四边形的判定与性质、菱形的判定等知识;本题综合性强,难度较大,需要多次证明三角形全等和等边三角形才能得出结论.