题目内容
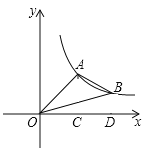
【题目】如图,在△ABC中,AB=AC=5,BC=6,在△ABC中截出一个矩形DEFG,使得点D在AB边上,EF在BC边上,点G在AC边上,设EF=x,矩形DEFG的面积为y.
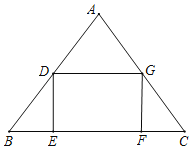
(1)求出y与x之间的函数关系式;
(2)直接写出自变量x的取值范围_______;
(3)若DG=2DE,则矩形DEFG的面积为_______.
【答案】(1)y=﹣![]() x2+4x;(2)0<x<6;(3)
x2+4x;(2)0<x<6;(3)![]() .
.
【解析】
(1)过点A作AN⊥BC于点N,交DG于点M,利用勾股定理和等腰三角形的三线合一求出BN、AN的长,由DG//BC可证明△ADG∽△ABC,得出比例线段,利用x表示出MN,利用矩形的面积求出函数解析式;(2)由题意即可得出答案;(3)由题意得出x=2(4﹣![]() x),解得x=
x),解得x=![]() ,代入函数关系式即可得出答案.
,代入函数关系式即可得出答案.
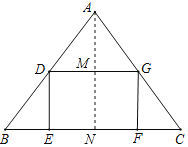
(1)如图,过点A作AN⊥BC于点N,交DG于点M,
∵AB=AC=5,BC=6,AN⊥BC,
∴BN=CN=3,AN=![]() =
=![]() =4,
=4,
∵DG∥BC,
∴△ADG∽△ABC,
∴![]() =
=![]() ,
,
∵DG=EF,
∴![]() =
=![]() ,
,
∴MN=4﹣![]() x.
x.
∴y=EFMN=x(4﹣![]() x)=﹣
x)=﹣![]() x2+4x,
x2+4x,
(2)∵0<EF<BC,
∴0<x<6;
故答案为:0<x<6
(3)∵DG=2DE,
∴EF=2MN,
∴x=2(4﹣![]() x),
x),
解得:x=![]() ,
,
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+4×
)2+4×![]() =
=![]() ,
,
∴矩形DEFG的面积为![]() ,
,
故答案为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目