题目内容
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,
为原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() .
.
(1)如图①,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 点,求
点,求![]() 点的坐标;
点的坐标;
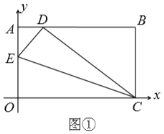
(2)如图②,在![]() 、
、![]() 边上选取适当的点
边上选取适当的点![]() 、
、![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上
边上![]() 点,过
点,过![]() 作
作![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,设
点,设![]() 的坐标为
的坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;

(3)在(2)的条件下,若![]() ,求
,求![]() 的面积.(直接写出结果即可)
的面积.(直接写出结果即可)
【答案】(1)![]() (2)
(2)![]() (
(![]() ) (3)
) (3)![]()
【解析】
(1)由折叠的性质可知![]() ,然后设
,然后设![]() ,在
,在![]() 中利用勾股定理即可求出m的值,从而可确定E点的坐标;
中利用勾股定理即可求出m的值,从而可确定E点的坐标;
(2)连接OT,由折叠的性质可知![]() ,然后在
,然后在![]() 中利用勾股定理即可得到
中利用勾股定理即可得到![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)先根据OG的长度求出![]() 的长度,然后设
的长度,然后设![]() ,则
,则![]() ,在
,在![]() 中,利用勾股定理即可求出x的值,最后利用
中,利用勾股定理即可求出x的值,最后利用![]() 即可求解.
即可求解.
解:(1)∵四边形OABC是矩形,
∴![]() .
.
设![]() ,则
,则![]() ,
,
由折叠的性质可知![]() ,
,![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)连接![]() ,
,

由折叠的性质可知![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,即
,即![]() ,
,
自变量![]() 的取值范围是
的取值范围是![]() .
.
(3)∵![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() .
.
由折叠的性质可知![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
解得![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目