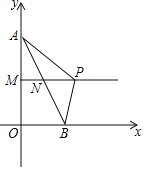题目内容
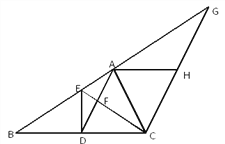
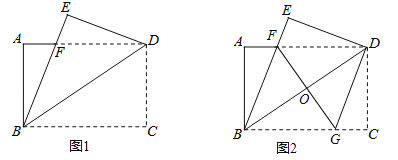
【题目】如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE 交 AD 于点 F.
(1)求证:△BDF 是等腰三角形;
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;
②若 AB=6,AD=8,则 FG 的长为_____.


【答案】![]()
【解析】试题分析:(1)证明△BDF是等腰三角形,可证明BF=DF,可通过证明∠EBD=∠FDB实现,利用折叠的性质和平行线的性质解决.
(2)①先判断四边形BFDG是平行四边形,再由(1)BF=FD得到结论;
②要求FG的长,可先求出OF的长,在Rt△BFO中,BO可由AB、AD的长及菱形的性质求得,解决问题的关键是求出BF的长.在Rt△BFA中,知AB=6、AF+BF=AD=8,可求出BF的长,问题得以解决.
试题解析:解:∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠CBD,由折叠的性质可知:∠EBD=∠CBD,∴ADB=∠EBD,∴BF=FD,∴△BDF是等腰三角形;
(2)①四边形BFDG是菱形.理由:
∵FD∥BG,DG∥BE,∴四边形BFDG是平行四边形.
又∵BF=DF,∴四边形BFDG是平行四边形;
②设AF=x,则FD=8﹣x,∴BF=FD=8﹣x.
在Rt△ABF中,62+x2=(8﹣x)2,解得:x=![]() ,∴FD=8﹣
,∴FD=8﹣![]() =
=![]() .在Rt△ABD中,∵AB=6,AD=8,∴BD=10.
.在Rt△ABD中,∵AB=6,AD=8,∴BD=10.
∵四边形BFDG是菱形,∴OD=![]() BD=5,FO=
BD=5,FO=![]() FG,FG⊥BD.在Rt△ODF中,∵FO2+DO2=FD2,即FO2+52=(
FG,FG⊥BD.在Rt△ODF中,∵FO2+DO2=FD2,即FO2+52=(![]() )2,∴FO=
)2,∴FO=![]() ,∴FG=2FO=
,∴FG=2FO=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某超市销售每台进价分别为200元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 3台 | 5台 | 1900元 |
第二周 | 4台 | 10台 | 3200元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
⑴求A、B两种型号的电风扇的销售单价;
⑵若超市准备用不多于5000元的金额再采购这两种型号的电风扇共30台,且按(1)中的销售单价全部售完利润不少于1850元,则有几种购货方案?
⑶在⑵的条件下,超市销售完这30台电风扇哪种方案利润最大?最大利润是多少?请说明理由.