Question

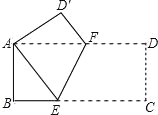
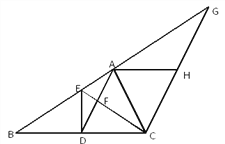
【题目】在△ABC中，D是BC的中点，且AD＝AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．过C点作CG∥AD，交BA的延长线于G，过A作BC的平行线交CG于H点．

（1）若∠BAC＝900，求证：四边形ADCH是菱形；

（2）求证：△ABC∽△FCD；

（3）若DE＝3，BC＝8，求△FCD的面积．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】试题分析：（1）首先判定四边形ADCH是平行四边形，然后由直角三角形斜边上的中线等于斜边的一边判定AD=CD，则易推知结论

（2）由AD=AC，可推出∠ADC=∠ACD；因为ED垂直平分BC，所以BE=CE，进而可得∠ECB=∠B，所以△ABC∽△FCD；

（3）首先过A作AG⊥CD，垂足为G，易得△BDE∽△BGA，可求得AG的长，继而求得△ABC的面积，然后由相似三角形面积比等于相似比的平方，求得△FCD的面积．

(1)证明：∵CG∥AD,AH∥CD，

∴四边形ADCH是平行四边形。

∵∠BAC=90°，D是BC的中点，

∴AD=CD，

∴四边形ADCH是菱形；

(2)∵AD=AC，

∴∠ADC=∠ACD，

∵D是BC的中点，DE⊥BC，

∴BE=CE，

∴∠B=∠FCD，

∴△ABC∽△FCD;

(3)过A作AM⊥CD，垂足为M.

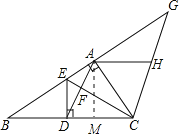
∵AD=AC，

∴DM=CM，

∴BD:BM=2:3，

∵ED⊥BC，

∴ED∥AM，

∴△BDE∽△BMA，

∴ED:AM=BD:BM=2:3，

∵DE=3，

∴AM=4.9，

∵△ABC∽△FCD，BC=2CD，

∴.

∵S△ABC=×BC×AM=×8×4.5=18，

∴S△FCD=S△ABC=.