Question

【题目】如图，BE、CF分别是钝角△ABC（∠A>90°）的高，在BE上截取BP＝AC，在CF的延长线截取CQ＝AB，连结AP、AQ，请推测AP与AQ的数量和位置关系并加以证明。

Answer 1

【答案】AP＝AQ，AP⊥AQ，理由见解析

【解析】

先证明△APB≌△QAC，得AP=AQ，∠BAP＝∠CQA，通过等量代换得∠BAP+∠QAF＝90°即可得AP⊥AQ．

解：AP＝AQ，AP⊥AQ，理由如下：

∵CF⊥AB，BE⊥AC，

∴∠AEB＝∠AFC＝90°，

∴∠ABE＝∠ACQ＝∠BAC﹣90°．

∵BP＝AC，CQ＝AB，

在△APB和△QAC中，

，

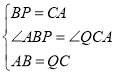∴△APB≌△QAC（SAS）．

∴∠BAP＝∠CQA，AP＝AQ，

∵∠CQA+∠QAF＝90°，

∴∠BAP+∠QAF＝90°．

即AP⊥AQ．