题目内容
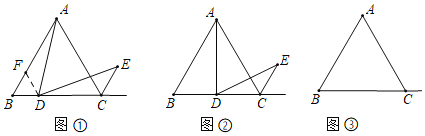
【题目】一节数学课后,老师布置了一道课后练习:△ABC是等边三角形,点D是线段BC上的点,点E为△ABC的外角平分线上一点,且∠ADE=60°,如图①,当点D是线段BC上(除B,C外)任意一点时,求证:AD=DE
(1)理清思路,完成解答
本题证明思路可以用下列框图表:

根据上述思路,请你完整地书写本题的证明过程;
(2)特殊位置,计算求解
当点D为BC的中点时,等边△ABC的边长为6,求出DE的长;
(3)知识迁移,探索新知
当点D在线段BC的延长线上,且满足CD=BC时,若AB=2,请直接写出△ADE的面积(不必写解答过程)
【答案】(1)见解析;(2)3![]() ;(3)3
;(3)3![]() .
.
【解析】
(1)由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(2)解直角三角形求出AD即可解决问题.
(3)只要证明∠BAD=90°,利用勾股定理求出AD,再证明△ADE是等边三角形即可解决问题.
(1)证明:如图①中,过点D作DF∥AC,交AB于点F.
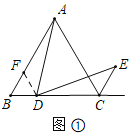
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠FAD=∠EDC,
在△AFD≌△DCE中,
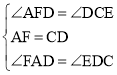 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE.
(2)如图②中,
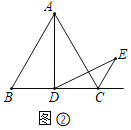
∵△ABC是等边三角形,
∴AB=AC=BC=6,
∵BD=DC=3,
∴AD⊥BC,
∴∠ADB=90°,
∴AD=![]() =3
=3![]() ,
,
由(1)可知:DE=AD=3![]() .
.
(3)如图3中,

∵CA=CD=CB=2,
∴∠BAD=90°,
∴AD=![]() =2
=2![]() ,
,
∵∠ADE=60°,∠ADB=30°,
∴∠BAD=∠EDC=90°,
∵ECD=60°,
∴DE=CDtan60°=2![]() ,
,
∴AD=DE,
∴△ADE是等边三角形,
∴S△ADE=![]() ×(2
×(2![]() )2=3
)2=3![]() .
.