题目内容
【题目】下列图案由边长相等的黑，白两色正方形按一定规律拼接而成，设第
个图案中白色小正方形的个数为
.
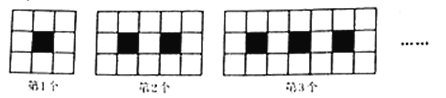
（1）第2个图案中有______个白色的小正方形；第3个图案中有______个白色的小正方形；与之间的函数表达式为______（直接写出结果）.
（2）是否存在这样的图案，使白色小正方形的个数为2019个？如果存在，请指出是第几个图案；如果不存在，说明理由.
【答案】（1）13；18；
；（2）不存在这样的图案，使得白色正方形的个数是2019个.
【解析】
（1）依据图形中黑，白两色正方形的数量，即可得到答案，进而得出y与x之间的函数表达式；
（2）解方程5x+3=2019，即可得到x的值，进而得出结论．
解：（1）第2个图案中白色的小正方形有3+5×2=13（个），
第3个图案中白色的小正方形有3+5×3=18（个），
y与x之间的函数表达式为y=5x+3，
故答案为：13，18，y=5x+3；
（2）依题意得，5x+3=2019，
解得x=403.2（不是整数），
∴不存在这样的图案，使白色小方形的个数为2019个．
练习册系列答案
相关题目
【题目】20筐白菜，以每筐18千克为标准，超过或不足的千克数分别用正、负数来表示．记录如下：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 2 | 3 | 2 | 1 | 4 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐重 千克．
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价1.3元，则出售这20筐白菜可卖多少元？
