题目内容
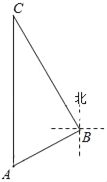
【题目】在△ABC中,∠ACB=90°,AC=8,BC=6,点D是射线CB上一动点,以每秒2个单位长度的速度从C出发向B运动,以CA,CD为边作矩形ACDE,直线AB与直线CE、DE的交点分别为F,G.设点D运动的时间为t(s).
(1)BD= (用含t的代数式表示).
(2)当四边形ACDE是正方形时,求GF的长.
(3)当t为何值时,△DFG为等腰三角形?
【答案】(1)6﹣2t或2t﹣6;(2)![]() ;(3)满足条件的t的值为2或
;(3)满足条件的t的值为2或![]() .
.
【解析】
(1)分两种情形分别求解即可.
(2)构建方程求出![]() 的值,再利用平行线分线段成比例定理求出
的值,再利用平行线分线段成比例定理求出![]() ,
,![]() ,
,![]() 即可解决问题.
即可解决问题.
(3)分两种情形:如图2中,当![]() 时,如图3中,当
时,如图3中,当![]() 时分别构建方程求解即可.
时分别构建方程求解即可.
解:(1)由题意:当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
故答案为![]() 或
或![]() .
.
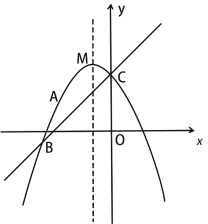
(2)如图1中,
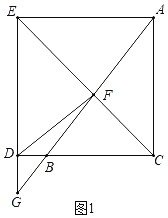
当四边形![]() 是正方形,
是正方形,![]() ,
,
可得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
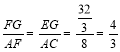 ,
,
![]() .
.
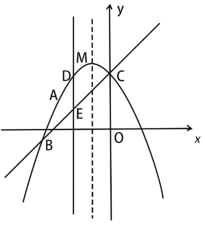
(3)如图2中,当![]() 时,
时,
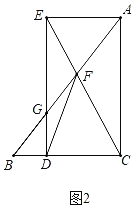
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
如图3中,当![]() 时,过点
时,过点![]() 作
作![]() 于
于![]() .
.
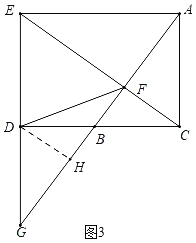
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
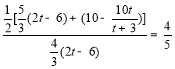 ,
,
解得![]() 或
或![]() ,
,
综上所述,满足条件的![]() 的值为2或
的值为2或![]() .
.

练习册系列答案
相关题目
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
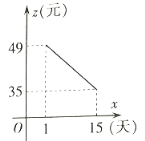
请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?