题目内容
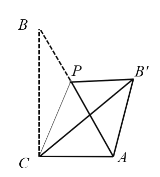
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
【答案】①②④
【解析】
由折叠的性质及直角三角形的性质对结论一一判断即可.
解:①AC=1,∠B=30°可知BC=![]() ,由翻折可知:B′C=BC=
,由翻折可知:B′C=BC=![]() ,
,
因为AB'⊥AC,由勾股定理可知:
AB'=![]() =
=![]() ,正确.
,正确.
②当点P位于AB中点时,CP=PB=PA=AC=PB′,∠B'PA=PAC=60°,PB'∥AC,
所以四边形ACPB'是平行四边形,
又PC=AC,
所以四边形ACPB'是菱形,正确.
③当∠B'PA=30°时,可知四边形BCB′P是菱形,BP=BC=![]() ;AP=2-
;AP=2-![]() ,
,
![]() 成立,故不正确.
成立,故不正确.
④当CP⊥AB时,∠B'=∠B'CA=30°,AC=AB',∠ACP=∠B=30°,
设AP=a,则AB'=AC=2a;AB=4a,PB=3a;
所以:AP:AB':BP=a:2a:3a=1:2:3,正确.
故答案为:①②④.

练习册系列答案
相关题目