Question

【题目】对于平面内的∠M和∠N，若存在一个常数k＞0，使得∠M＋k∠N＝360°，则称∠N为∠M的k系补周角．如若∠M＝90°，∠N＝45°，则∠N为∠M的6系补周角．

（1）若∠H＝120°，则∠H的4系补周角的度数为 ；

（2）在平面内AB∥CD，点E是平面内一点，连接BE，DE．

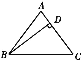
①如图1，∠D＝60°，若∠B是∠E的3系补周角，求∠B的度数；

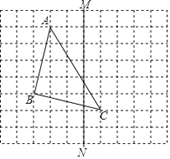
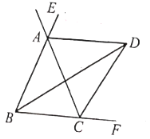
②如图2，∠ABE和∠CDE均为钝角，点F在点E的右侧，且满足∠ABF=n∠ABE，∠CDF=n∠CDE（其中n为常数且n＞1），点P是∠ABE角平分线BG上的一个动点，在P点运动过程中，请你确定一个点P的位置，使得∠BPD是∠F的k系补周角，并直接写出此时的k值（用含n的式子表示）．

Answer 1

【答案】（1）60°；（2）①75°，②当BG上的动点P为∠CDG的角平分线与BG的交点时，满足∠BPD是∠F的k系补周角，此时k=2n，推导见解析.

【解析】

（1）直接利用k系补周角的定义列方程求解即可．

（2）①依据k系补周角的定义及平行线的性质，建立∠BED、∠B、∠D的关系式求解即可.

②结合本题的构图特点，利用平行线的性质得到：∠ABF+∠CDF+∠F=360°,结合∠ABF=n∠ABE，∠CDF=n∠CDE（其中n为常数且n＞1），又由于点P是∠ABE角平分线BG上的一个动点，通过构造相同特殊条件猜想出一个满足条件的P点，再通过推理论证得到k的值（含n的表达式），即说明点P即为所求.

解：（1）设∠H的4系补周角的度数为x，

则有120°+4x=360°，

解得：x=60°

∴∠H的4系补周角的度数为60°；

（2）①如图，

过点E作EF//AB，

∵AB//EF,

∴EF//CD，

∴∠B=∠1,∠D=∠2，

∴∠1+∠2=∠B+∠D，

即∠BED=∠B+∠D，

∵∠BED+3∠B=360°，∠D＝60，

∴，

解得：∠B=75°，

∴∠B=75°；

②预备知识，基本构图：

如图，AB//CD//EF,则

∠ABE+∠BEG=180°，

∠DCE+∠GEC=180°，

∴∠ABE+∠BEG+∠DCE+∠GEC=360°，

即∠ABE+∠DCG+∠BEC=360°

如图：

当BG上的动点P为∠CDG的角平分线与BG的交点时，满足∠BPD是∠F的k系补周角，此时k=2n.理由如下：

若∠BPD是∠F的k系补周角，则

∠F+k∠BPD=360°，

∴k∠BPD=360°-∠F

又由基本构图知：

∠ABF+∠CDF=360°-∠F，

∴k∠BPD=∠ABF+∠CDF，

又∵∠ABF=n∠ABE，∠CDF=n∠CDE，

∴k∠BPD= n∠ABE+ n∠CDE，

∵∠BPD=∠PHD+∠PDH,

∵AB//CD，PG平分∠ABE，PD平分∠CDE，

∴∠PHD=∠ABH= ,∠PDH=，

∴(+)=n(∠ABE+∠CDE)，

∴k=2n.