题目内容
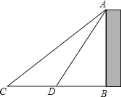
【题目】如图所示，已知
是等腰
底边上的高，且
，
上有一点
，满足
，则
的值是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
过E点作CD的平行线交AD于F，设AE=2a，则CE=3a．tan∠C=
，EF和DF分别可用a的代数式来表达，即可得出tan∠ADE的值．
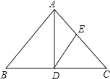
过E点作CD的平行线交AD于F．如图：
∵AD是等腰△ABC底边上的高，tan∠B=，∴EF⊥AD，tan∠C=tan∠B=．
设AE=2a．
∵AE：CE=2：3，∴CE=3a，AC=5a．
∵tan∠C=，∴sin∠C=
，cos∠C=
．
在直角△ADC中，AD=ACsin∠C=5a×=3a．
在直角△AFE中，AF=AE×sin∠AEF=AE×sin∠C=2a×=
．
EF=AE×cos∠AEF=AE×cos∠C=2a×=
．
在直角△DFE中，tan∠ADE=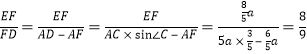
．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
【题目】酒泉市教育局计划对全市八年级学生学习情况进行调查，随机从全市抽取城市和农村两组学生的期中数学成绩，每组10人进行对比分析．绘制统计图如下．根据图中信息，完成下列问题．
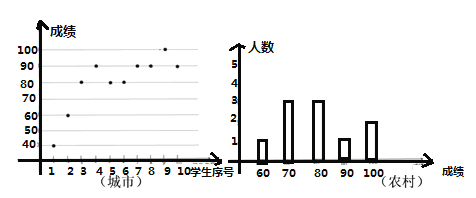
（1）完成下表；
平均数 | 中位数 | 众数 | 方差 | |
城市 | ||||
农村 |
（2）依据上表的信息谈谈你的看法．
