题目内容
【题目】如图, ![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和正三角形
和正三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,以下五个结论:①
,以下五个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,一定成立的是( )
,一定成立的是( )

A.①②③④
B.①②④⑤
C.①②③⑤
D.①③④⑤
【答案】B
【解析】
根据等边三角形的性质可以得出E△ACE≌△DCB,就可以得出∠CAE=∠CDB,∠AEC=∠DBC,通过证明△CEG≌△CBH就可以得出CG=CH,GE=HB,可以得出△GCH是等边三角形,就可以得出∠GHC=60°,就可以得出GH//AB,由∠DCH≠∠DHC就可以得出CD≠DH,就可以得出AD≠DH,根据∠AFD=∠EAB+∠CBD=∠CDB+∠CBD=∠ACD=60°,进而得出结论.
解:∵△ACD和△BCE是等边三角形,
∴AD=AC=CD,CE=CB=BE,∠ACD=∠BCE=60°.
∵∠ACB=180°,
∴∠DCE=60°.
∴∠DCE=∠BCE.
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB.
在△ACE和△DCB中,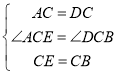 ,
,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAE=∠CDB,∠AEC=∠DBC.
在△CEG和△CBH中,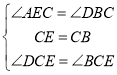 ,
,
∴△CEG≌△CBH(ASA),
∴CG=CH,GE=HB,
∴△CGH为等边三角形,
∴∠GHC=60°,
∴∠GHC=∠BCH,
∴GH//AB.
∵∠AFD=∠EAB+∠CBD,
∴∠AFD=∠CDB+∠CBD=∠ACD=60°.
∵∠DHC=∠HCB+∠HBC=60°+∠HBC,∠DCH=60°
∴∠DCH≠∠DHC,
∴CD≠DH,
∴AD≠DH.
综上所述,正确的有:①②④⑤.
故选B.

【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?