题目内容
【题目】定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
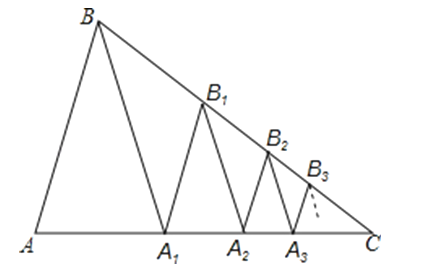
如图,已知△ABC中,AC=BC,∠C=36°,BA1平分∠ABC交AC于A1 . 
(1)证明:AB2=AA1AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1 , B1A2平分∠A1B1C交AC于A2 , 作A2B2∥AB交B2 , B2A3平分∠A2B2C交AC于A3 , 作A3B3∥AB交BC于B3 , …,依此规律操作下去,用含a,n的代数式表示An﹣1An . (n为大于1的整数,直接回答,不必说明理由)
【答案】
(1)
证明:∵AC=BC,∠C=36°,
∴∠A=∠ABC=72°,
∵BA1平分∠ABC,
∴∠ABA1=![]() ∠ABC=36°,
∠ABC=36°,
∴∠C=∠ABA1,
又∵∠A=∠A,
∴△ABC∽△AA1B,
∴![]() =
=![]() ,即AB2=AA1AC;
,即AB2=AA1AC;
(2)
解:△ABC是黄金等腰三角形,
理由:由(1)知,AB2=ACAA1,
设AC=1,
∴AB2=AA1,
又由(1)可得:AB=A1B,
∵∠A1BC=∠C=36°,
∴A1B=A1C,
∴AB=A1C,
∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,
∴AB2=1﹣AB,
设AB=x,即x2=1﹣x,
∴x2+x﹣1=0,
解得:x1=![]() ,x2=
,x2=![]() (不合题意舍去),
(不合题意舍去),
∴AB=![]() ,
,
又∵AC=1,
∴![]() =
=![]() ,
,
∴△ABC是黄金等腰三角形;
(3)
解:由(2)得;当AC=a,则AA1=AC﹣A1C=AC﹣AB=a﹣AB=a﹣![]() a=
a=![]() a,
a,
同理可得:A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1
=a﹣![]() a﹣
a﹣![]() A1C
A1C
=a﹣![]() a﹣
a﹣![]() [a﹣
[a﹣![]() a]
a]
=![]() a.
a.
故An﹣1An=![]() a.
a.
【解析】

练习册系列答案
相关题目