Question

【题目】如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．

（1）若∠B=60°，这时点P与点C重合，则∠NMP= 度
（2）求证：NM=NP
（3）当△NPC为等腰三角形时，求∠B的度数

Answer 1

【答案】
（1）30
（2）

证明：延长MN交DC的延长线于点E，

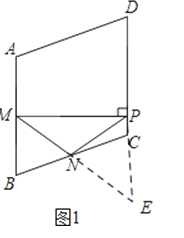
∵四边形ABCD是菱形，∴AB∥DC，

∴∠BMN=∠E，

∵点N是线段BC的中点，∴BN=CN，

在△MNB和△ENC中，

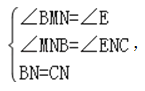
∴△MNB≌△ENC，

∴MN=EN，

即点N是线段ME的中点，

∵MP⊥AB交边CD于点P，

∴MP⊥DE，

∴∠MPE=90°，

∴PN=MN=ME

（3）

解：如图2

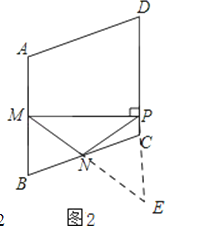
∵四边形ABCD是菱形，∴AB=BC，

又M，N分别是边AB，BC的中点，

∴MB=NB，

∴∠BMN=∠BNM，

由（2）知：△MNB≌△ENC，

∴∠BMN=∠BNM=∠E=∠CNE，

又∵PN=MN=NE，

∴∠NPE=∠E，

设∠BMN=∠BNM=∠E=∠CNE=∠NPE=x°，

则∠NCP=2x°，∠NPC=x°，

①若PN=PC，则∠PNC=∠NCP=2x°，

在△PNC中，2x+2x+x=180，

解得：x=36，

∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°，

②若PC=NC，则∠PNC=∠NPC=x°，

在△PNC中，2x+x+x=180，

解得：x=45，

∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°．

【解析】（1）根据直角三角形的中线等于斜边上的一半，即可得解；
（2）延长MN交DC的延长线于点E，证明△MNB≌△ENC，进而得解；
（3）NC和PN不可能相等，所以只需分PN=PC和PC=NC两种情况进行讨论即可．
此题考查了直角三角形中线，全等三角形判定与性质.