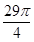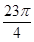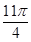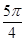题目内容
如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,取CB的中点E,DE的延长线与AB的延长线交于点P.
(1)求证:PD是⊙O的切线;
(2)若OB=BP,AD=6,求BC的长;
(3)如图2,连接OD,AE相交于点F,若tan∠C=2,求 的值.
的值.


图1 图2
(1)求证:PD是⊙O的切线;
(2)若OB=BP,AD=6,求BC的长;
(3)如图2,连接OD,AE相交于点F,若tan∠C=2,求
 的值.
的值.

图1 图2
(1)证明见解析;
(2)BC=4;
(3) .
.
(2)BC=4;
(3)
 .
.试题分析:(1)连接BD、DO,OE,只要证明∠ODE=90°,OD是半径,就可得到DE是⊙O的切线;
(2)根据△ADB∽△BDC,从而根据相似比不难求得BD的长;
(3)根据平行线分线段成比例进行分析.
试题解析:(1)如图1,连接BD,OD,OE.

∵AB是直径,
∴∠ADB=∠CDB=90°.
∵E是BC中点,
∴DE=EC=EB,
又∵OD=OB,OE=OE,
∴△ODE≌△OBE(SSS),
∴∠ODE=∠OBE=90°,
∴OD⊥DP,
∴PD是⊙O的切线;
(2)∵OB=BP,∠ODP=90°,
∴DB=OB=BP,即DB=OB=OD.
∴△ODB是等边三角形.
∴∠DOB=60°.
∴∠A=30°,
又∵∠ABC=90°,
∴∠C=60°.
∴∠CBD=30°.
∴
 ,
, ,
,设
 ,
, ,
,∵AD=6,
∴
 .
.∴
 .
.∴BC=4;
(3)如图2,连接BD,OE.

∵tan∠C=2,∠CDB=90°,
∴
 =2.
=2.又∵∠ABD=∠C=60°,
∴
 =2,
=2,设
 ,
, ,
, ,
,∴AC=
 .
.∵O是AB中点,E是BC中点,
∴
 ,
,∴
 ,
, ∴
 .
.
练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
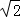 ,求AE的长.
,求AE的长.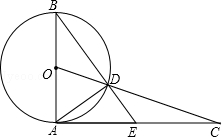
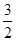 ,tanF=
,tanF=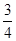 ,求⊙O的半径.
,求⊙O的半径.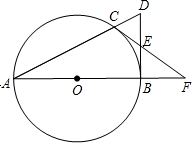
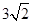
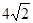
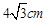 B、
B、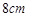 8cm C、
8cm C、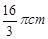 D、
D、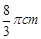
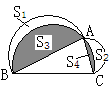
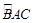 ,如图所示,若AB=4,AC=2,
,如图所示,若AB=4,AC=2,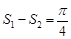 ,则S3-S4的值是( )
,则S3-S4的值是( )