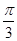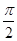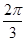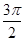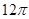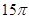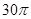题目内容
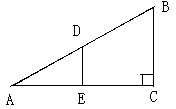
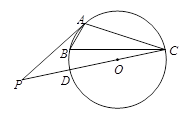
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.
(1)求证:CF是⊙O的切线;
(2)若ED=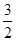 ,tanF=
,tanF=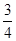 ,求⊙O的半径.
,求⊙O的半径.
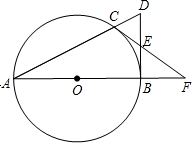
(1)求证:CF是⊙O的切线;
(2)若ED=
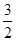 ,tanF=
,tanF=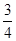 ,求⊙O的半径.
,求⊙O的半径.
(1)证明见解析;(2)3.
试题分析:(1)连CB、OC,根据切线的性质得∠ABD=90°,根据圆周角定理由AB是直径得到∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,所以∠BCE=∠CBE,所以∴OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是⊙O的切线.
(2)CE=BE=DE=
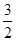 ,在Rt△BFE中,利用正切的定义得
,在Rt△BFE中,利用正切的定义得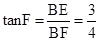 ,可计算出BF=2,再利用勾股定理可计算出EF=
,可计算出BF=2,再利用勾股定理可计算出EF=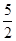 ,所以CF=CE+EF=4,然后在Rt△OCF中,利用正切定义可计算出OC.
,所以CF=CE+EF=4,然后在Rt△OCF中,利用正切定义可计算出OC.试题解析:(1)如图,连接CB、OC,
∵BD为⊙O的切线,∴DB⊥AB。∴∠ABD=90°.
∵AB是直径,∴∠ACB=90°.
∴∠BCD=90°.
∵E为BD的中点,∴CE="BE." ∴∠BCE=∠CBE.
而∠OCB=∠OBC,
∴∠OBC+∠CBE=∠OCB+∠BCE=90°.
∴OC⊥CF,
∴CF是⊙O的切线;
(2)解:CE=BE=DE=
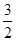 ,
,在Rt△BFE中,
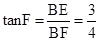 ,∴BF=2.
,∴BF=2.∴
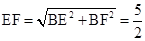 .∴CF=CE+EF=4.
.∴CF=CE+EF=4.在Rt△OCF中,
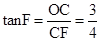 ,∴OC=3,即⊙O的半径为3.
,∴OC=3,即⊙O的半径为3.
练习册系列答案
相关题目
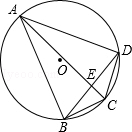
 的值.
的值.


 的长等于( )
的长等于( )