题目内容
 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.(1)求直线AC的解析式.
(2)用含t的代数式表示P的坐标
(6-t,
t)
| 4 |
| 3 |
(6-t,
t)
(直接写出答案)| 4 |
| 3 |
(3)是否存在点P使得
| S | 四边形OMPC |
| 39 |
| 2 |
(4)是否存在t的值,使以P、A、M为顶点的三角形与△AOC相似?若存在,请求t的值;若不存在,请说明理由.
分析:(1)根据矩形的性质求出C点坐标,利用待定系数法求出AC的解析式;
(2)求出CN的长度表达式即为P点横坐标,代入解析式即可求出P点的纵坐标,从而得到P点坐标表达式;
(3)存在,求出AM的长度表达式,根据三角形的面积公式求出△AMP的面积表达式,用△ACO的面积减去△AMP的面积表达式即为S四边形OMPC,使面积等于
,求出t的值,即可确定出此时P的坐标;
(3)先假设以P、A、M为顶点的三角形与△AOC相似,再根据相似三角形的性质进行计算,若能求出t,则存在;否则不存在.
(2)求出CN的长度表达式即为P点横坐标,代入解析式即可求出P点的纵坐标,从而得到P点坐标表达式;
(3)存在,求出AM的长度表达式,根据三角形的面积公式求出△AMP的面积表达式,用△ACO的面积减去△AMP的面积表达式即为S四边形OMPC,使面积等于
| 39 |
| 2 |
(3)先假设以P、A、M为顶点的三角形与△AOC相似,再根据相似三角形的性质进行计算,若能求出t,则存在;否则不存在.
解答:解:(1)∵四边形OABC为矩形,点A、B的坐标为(6,0),(6,8),
∴C点坐标为(0,8),
设AC的解析式为y=kx+b,
将A(6,0),C(0,8)代入y=kx+b得:
,
解得:
,
则直线AC的解析式为y=-
x+8;
(2)∵CN=6-t,
∴yP=-
(6-t)+8=
t,
则P点坐标为(6-t,
t);
故答案为:(6-t,
t)
(3)存在.
∵AM=AO-OM=6-t,
∴S△AMP=
×(6-t)×
t=-
t2+4t,
∴y=S四边形OMPC=S△AOC-S△AMP=
×6×8-(-
t2+4t)=
t2-4t+24=
(t-3)2+18,
当y=
时,有
(t-3)2+18=
,
解得:t=
或t=
,
则满足题意P的坐标为(
,2)或(
,6);
(4)存在.
在△ACB中,PN∥AB,
则
=
,
即
=
,
解得AP=
t,
又∵AM=6-t,
则有:①△AMP∽△AOC时,
=
,即
=
,解得t=3秒;
②△APM∽△AOC时,
=
,即
=
,解得t=
秒,
综上所述,当t=3秒或t=
秒时,以P、A、M为顶点的三角形与△AOC相似.
∴C点坐标为(0,8),
设AC的解析式为y=kx+b,
将A(6,0),C(0,8)代入y=kx+b得:
|
解得:
|
则直线AC的解析式为y=-
| 4 |
| 3 |
(2)∵CN=6-t,
∴yP=-
| 4 |
| 3 |
| 4 |
| 3 |
则P点坐标为(6-t,
| 4 |
| 3 |
故答案为:(6-t,
| 4 |
| 3 |
(3)存在.
∵AM=AO-OM=6-t,
∴S△AMP=
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
∴y=S四边形OMPC=S△AOC-S△AMP=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
当y=
| 39 |
| 2 |
| 2 |
| 3 |
| 39 |
| 2 |
解得:t=
| 3 |
| 2 |
| 9 |
| 2 |
则满足题意P的坐标为(
| 9 |
| 2 |
| 3 |
| 2 |
(4)存在.
在△ACB中,PN∥AB,
则
| BN |
| BC |
| AP |
| AC |
即
| t |
| 6 |
| AP |
| 10 |
解得AP=
| 5 |
| 3 |
又∵AM=6-t,
则有:①△AMP∽△AOC时,
| AM |
| AO |
| AP |
| AC |
| 6-t |
| 6 |
| ||
| 10 |
②△APM∽△AOC时,
| AP |
| AO |
| AM |
| AC |
| ||
| 6 |
| 6-t |
| 10 |
| 27 |
| 17 |
综上所述,当t=3秒或t=
| 27 |
| 17 |
点评:本题考查了动点问题与相似三角形的性质,根据题意,逐步解答,充分利用前一问题的结论是解题的关键,同时要注意分类讨论.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
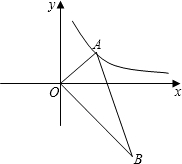 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2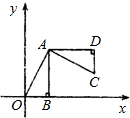 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
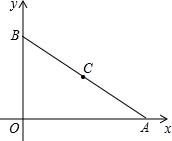 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.